题目内容
（2012•开封一模）已知点M（1，0）是圆C：x2+y2-4x-2y=0内一点，则过点M的最长弦所在的直线方程是
x-y-1=0
x-y-1=0
．分析：将圆C的方程化为标准方程，找出圆心C的坐标，根据M为圆C内一点，得到过M最长的弦为直径，由圆心C与M求出直径所在直线方程的斜率，即可得到直径所在直线的方程，即为过点M的最长弦所在的直线方程．
解答：解：将圆C的方程化为标准方程得：（x-2）2+（y-1）2=5，
∴圆心C（2，1），
又M（1，0）为圆C内一点，∴过点M的最长弦为圆C的直径，
则过点M的最长弦所在的直线方程是y=
（x-1），即x-y-1=0．
故答案为：x-y-1=0
∴圆心C（2，1），
又M（1，0）为圆C内一点，∴过点M的最长弦为圆C的直径，
则过点M的最长弦所在的直线方程是y=
| 1-0 |
| 2-1 |
故答案为：x-y-1=0
点评：此题考查了直线与圆的位置关系，涉及的知识有：圆的标准方程，直线的两点式方程，其中得出过点M的最长弦为圆C的直径是解本题的关键．
练习册系列答案
相关题目
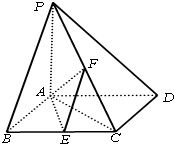（2012•开封一模）已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．