题目内容
(文)若 =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),其中ω>0,记函数f(x)=(
=(sinωx,0),其中ω>0,记函数f(x)=( +
+ )•
)• +k.
+k.
(1)若函数f(x)的图象中相邻两条对称轴间的距离不小于 ,求ω的取值范围;
,求ω的取值范围;
(2)若函数f(x)的最小正周期为π,且当x∈[- ,
, ]时,函数f(x)的最大值是
]时,函数f(x)的最大值是 ,求函数f(x)的解析式,并说明如何由函数y=sinx的图象变换得到函数y=f(x)的图象.
,求函数f(x)的解析式,并说明如何由函数y=sinx的图象变换得到函数y=f(x)的图象.
解:∵ =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),
=(sinωx,0),
∴ +
+ =(
=( cosωx+sinωx,sinωx).
cosωx+sinωx,sinωx).
故f(x)=( +
+ )•
)• +k=
+k= sinωxcosωx+sin2ωx+k
sinωxcosωx+sin2ωx+k
= sin2ωx+
sin2ωx+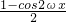 +k=
+k= sin2ωx-
sin2ωx- cos2ωx+
cos2ωx+ +k
+k
=sin(2ωx- )+k+
)+k+ .
.
(1)由题意可知 =
=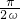 ≥
≥ ,∴ω≤1.
,∴ω≤1.
又ω>0,∴0<ω≤1.
(2)∵T= =π,∴ω=1.
=π,∴ω=1.
∴f(x)=sin(2x- )+k+
)+k+ .
.
∵x∈[- ,
, ],∴2x-
],∴2x- ∈[-
∈[- ,
, ].
].
从而当2x- =
= ,即x=
,即x= 时,f(x)max=f(
时,f(x)max=f( )=sin
)=sin +k+
+k+ =k+1=
=k+1= ,
,
∴k=- .故f(x)=sin(2x-
.故f(x)=sin(2x- ).
).
由函数y=sinx的图象向右平移 个单位长度,得到函数y=sin(x-
个单位长度,得到函数y=sin(x- )的图象,再将得到的函数图象上所有点的横坐标变为原来的
)的图象,再将得到的函数图象上所有点的横坐标变为原来的 倍(纵坐标不变),得到函数y=sin(2x-
倍(纵坐标不变),得到函数y=sin(2x- )的图象.
)的图象.
分析:利用向量的数量积,化简函数的表达式,通过二倍角、两角差的正弦函数化简函数为一个角的一个三角函数的形式,
(1)利用周期与函数f(x)的图象中相邻两条对称轴间的距离不小于 ,得到关系式,求出ω的取值范围;
,得到关系式,求出ω的取值范围;
(2)通过周期求出ω,通过函数的最大值,求出x的值,然后确定k的值.利用函数图象平移的原则:左加右减,上加下减由函数y=sinx的图象变换得到函数y=f(x)的图象.
点评:本题是中档题,考查三角函数的化简、公式的应用、周期的求法、最值的应用及函数图象的变换,还考查发现问题解决问题的能力、计算能力,是常考题型.
 =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),
=(sinωx,0),∴
 +
+ =(
=( cosωx+sinωx,sinωx).
cosωx+sinωx,sinωx).故f(x)=(
 +
+ )•
)• +k=
+k= sinωxcosωx+sin2ωx+k
sinωxcosωx+sin2ωx+k=
 sin2ωx+
sin2ωx+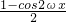 +k=
+k= sin2ωx-
sin2ωx- cos2ωx+
cos2ωx+ +k
+k=sin(2ωx-
 )+k+
)+k+ .
.(1)由题意可知
 =
=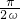 ≥
≥ ,∴ω≤1.
,∴ω≤1.又ω>0,∴0<ω≤1.
(2)∵T=
 =π,∴ω=1.
=π,∴ω=1.∴f(x)=sin(2x-
 )+k+
)+k+ .
.∵x∈[-
 ,
, ],∴2x-
],∴2x- ∈[-
∈[- ,
, ].
].从而当2x-
 =
= ,即x=
,即x= 时,f(x)max=f(
时,f(x)max=f( )=sin
)=sin +k+
+k+ =k+1=
=k+1= ,
,∴k=-
 .故f(x)=sin(2x-
.故f(x)=sin(2x- ).
).由函数y=sinx的图象向右平移
 个单位长度,得到函数y=sin(x-
个单位长度,得到函数y=sin(x- )的图象,再将得到的函数图象上所有点的横坐标变为原来的
)的图象,再将得到的函数图象上所有点的横坐标变为原来的 倍(纵坐标不变),得到函数y=sin(2x-
倍(纵坐标不变),得到函数y=sin(2x- )的图象.
)的图象.分析:利用向量的数量积,化简函数的表达式,通过二倍角、两角差的正弦函数化简函数为一个角的一个三角函数的形式,
(1)利用周期与函数f(x)的图象中相邻两条对称轴间的距离不小于
 ,得到关系式,求出ω的取值范围;
,得到关系式,求出ω的取值范围;(2)通过周期求出ω,通过函数的最大值,求出x的值,然后确定k的值.利用函数图象平移的原则:左加右减,上加下减由函数y=sinx的图象变换得到函数y=f(x)的图象.
点评:本题是中档题,考查三角函数的化简、公式的应用、周期的求法、最值的应用及函数图象的变换,还考查发现问题解决问题的能力、计算能力,是常考题型.

练习册系列答案
相关题目
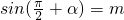 ,则cosα=________.
,则cosα=________.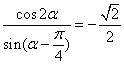 ,则cos
,则cos