题目内容
(文)若
,则目标函数z=x+2y的取值范围是
(理)将曲线
(θ∈R),上所有点的横坐标扩大到原来的2倍,纵坐标缩小到原来的
倍后,得到的曲线的焦点坐标为
|
[2,6],(±
,0)
| ||
| 2 |
[2,6],(±
,0)
.
| ||
| 2 |
(理)将曲线
|
| 1 |
| 2 |
(±
,0)
| ||
| 2 |
(±
,0)
.
| ||
| 2 |
分析:(文)画出
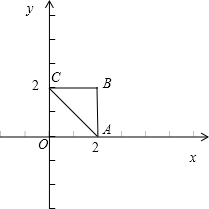
的可行域,则 A(2,0),B(2,2)是目标函数z=x+2y最优解.把 A(2,0),B(2,2)分别代入目标函数z=x+2y得到z的最小值和最大值,从而得到目标函数z=x+2y的取值范围.
(理)先将曲线
(θ∈R)上所有点的横坐标扩大到原来的2倍,纵坐标缩小到原来的
倍后,得到的曲线是
(θ∈R),再化成普通方程,表示焦点在x轴的椭圆,最后求得其焦点坐标即可.
|
(理)先将曲线
|
| 1 |
| 2 |
|
解答:解:(文)画出
的可行域,则 A(2,0),B(2,2)是目标函数z=x+2y最优解.
把 A(2,0),B(2,2)分别代入目标函数z=x+2y得到z=2和z=6,
故 2≤z≤6,即目标函数z=x+2y的取值范围是[2,6].
故答案为:[2,6].
(理)将曲线
(θ∈R) 上所有点的横坐标扩大到原来的2倍,纵坐标缩小到原来的
倍后,
得到的曲线是:
(θ∈R),其普通方程为:
+
=1,表示焦点在x轴的椭圆,
其a=2,b=
,c=
. 焦点坐标为(±
,0),
故答案为:(±
,0).
|
把 A(2,0),B(2,2)分别代入目标函数z=x+2y得到z=2和z=6,
故 2≤z≤6,即目标函数z=x+2y的取值范围是[2,6].
故答案为:[2,6].

(理)将曲线
|
| 1 |
| 2 |
得到的曲线是:
|
| x2 |
| 4 |
| y2 | ||
|
其a=2,b=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故答案为:(±
| ||
| 2 |
点评:本题主要考查线性规划问题,伸缩变换、椭圆的简单性质,考查运算求解能力,体现了数形结合的数学思想,
属于基础题.
属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 已知曲线C:x2-y|y|=1(|x|≤4).
已知曲线C:x2-y|y|=1(|x|≤4).