题目内容
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD= ![]() AD=1,E为棱AD的中点,M为棱PA的中点.
AD=1,E为棱AD的中点,M为棱PA的中点. 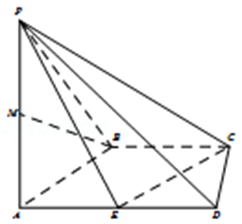
(1)求证:BM∥平面PCD;
(2)若∠ADP=45°,求二面角A﹣PC﹣E的余弦值.
【答案】
(1)证明:法一:取PD的中点N,连接MN,CN.
在△PAD中,N、M分别为棱PD、PA的中点∴ ![]()
∵ ![]() ∴四边形BCNM是平行四边形∴BM∥CN
∴四边形BCNM是平行四边形∴BM∥CN
∵BM平面PCD,CN平面PCD∴BM∥平面PCD…(5分)
(法二:连接EM,BE.
在△PAD中,E、M分别为棱AD、PA的中点∴MN∥PD
∵AD∥BC, ![]()
∴四边形BCDE是平行四边形∴BE∥CD∵BE∩ME=E,MN∥PD,BE∥CD
∴平面BEM∥平面PCD∵BM平面BEM∴BM∥平面PCD)

(2)以A为原点,以 ![]() ,
, ![]() 的方向分别为x轴,z轴的正方向建立空间直角坐标系A﹣xyz…(6分)
的方向分别为x轴,z轴的正方向建立空间直角坐标系A﹣xyz…(6分)
则A(0,0,0),C(2,1,0),E(1,0,0).
∵点P在底面ABCD上的射影为A
∴PA⊥平面ABCD
∵∠ADP=45°∴PA=AD=2
∴P(0,0,2)
∴ ![]() ,
, ![]() ,
, ![]()
设平面PAC的一个法向量 ![]() ,
,
则 ![]()
设a=1,则 ![]()
设平面PCE的一个法向量为 ![]() ,
,
则 ![]() ,
,
设x=2,则 ![]()
∴cos ![]() =
= ![]() =
= ![]()
由图知:二面角A﹣PC﹣E是锐二面角,设其平面角为θ,则
cosθ=|cos ![]() |=
|= ![]()

【解析】(1.)法一:取PD的中点N,连接MN,CN.证明BM∥CN,然后证明BM∥平面PCD. (法二:连接EM,BE.通过证明平面BEM∥平面PCD,然后证明BM∥平面PCD)(2.)以A为原点,以 ![]() ,
, ![]() 的方向分别为x轴,z轴的正方向建立空间直角坐标系A﹣xyz求出相关点的坐标,求出平面PAC的一个法向量,平面PCE的一个法向量,利用空间向量的数量积求解二面角A﹣PC﹣E的余弦函数值.
的方向分别为x轴,z轴的正方向建立空间直角坐标系A﹣xyz求出相关点的坐标,求出平面PAC的一个法向量,平面PCE的一个法向量,利用空间向量的数量积求解二面角A﹣PC﹣E的余弦函数值.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 | 开车时不使用手机 | 合计 | |
男性司机人数 | |||
女性司机人数 | |||
合计 |
(Ⅱ)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

