题目内容
已知 是周期为
是周期为 的函数,当x∈(
的函数,当x∈( )时,
)时, 设
设 则
则
| A.c<b<a | B.b<c<a | C.c<a<b | D.a<c<b |
D
解析试题分析:根据题意,由于 是周期为
是周期为 的函数,当x∈(
的函数,当x∈( )时,
)时, 那么
那么 由于f(-2)=f(-2+
由于f(-2)=f(-2+ ), f(-3)=f(-3+
), f(-3)=f(-3+ ),那么结合函数性质可知,函数的导数为
),那么结合函数性质可知,函数的导数为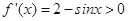 可知函数为增函数,故可知结论为a<c<b,故可知选D.
可知函数为增函数,故可知结论为a<c<b,故可知选D.
考点:函数的周期性
点评:主要是考查了函数的性质的运用,属于基础题。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
要得到函数 的图像,只需将
的图像,只需将 的图像( )
的图像( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
若一扇形的圆心角为 ,半径为20cm,则扇形的面积为( )
,半径为20cm,则扇形的面积为( )
A.40 cm2 cm2 | B.80 cm2 cm2 | C.40cm2 | D.80cm2 |
函数y=cosx( )的值域是( )
)的值域是( )
A. | B. | C. | D.[-1,1] |
如果函数 的图像关于点
的图像关于点 中心对称,那么
中心对称,那么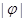 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
设 ,若函数
,若函数 在
在 上单调递增,则
上单调递增,则 的取值范围是________
的取值范围是________
A. | B. | C. | D. |
 ( )
( )
A. | B. | C. | D. |
已知正弦函数 的图象关于点
的图象关于点 对称,则
对称,则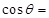
A.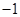 或 或 | B. | C.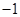 | D. |
 的是( )
的是( ) B
B C
C D
D