题目内容
已知正弦函数 的图象关于点
的图象关于点 对称,则
对称,则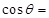
A.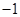 或 或 | B. | C.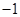 | D. |
A
解析试题分析:根据题意,由于正弦函数 的图象关于点
的图象关于点 对称,则说明了当x=
对称,则说明了当x= 时,值得有sin
时,值得有sin =0,即结合同角关系式可知
=0,即结合同角关系式可知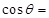
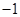 或
或 ,故答案为A
,故答案为A
考点:正弦函数的性质
点评:主要是考查了正弦函数的对称中心的运用,属于基础题。

练习册系列答案
相关题目
已知 是周期为
是周期为 的函数,当x∈(
的函数,当x∈( )时,
)时, 设
设 则
则
| A.c<b<a | B.b<c<a | C.c<a<b | D.a<c<b |
将分针拨快10分钟,则分针转过的弧度数是 ( )
A. | B. | C. | D. |
已知函数 ,则其图象的下列结论中,正确的是( )
,则其图象的下列结论中,正确的是( )
A.关于点 中心对称 中心对称 | B.关于直线 轴对称 轴对称 |
C.向左平移 后得到奇函数 后得到奇函数 | D.向左平移 后得到偶函数 后得到偶函数 |
下列命题正确的是 ( )
A.函数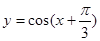 的图像是关于点 的图像是关于点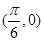 成中心对称的图形 成中心对称的图形 |
B.函数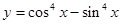 的最小正周期为2 的最小正周期为2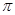 |
C.函数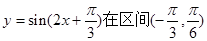 内单调递增 内单调递增 |
D.函数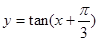 的图像是关于直线 的图像是关于直线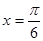 成轴对称的图形 成轴对称的图形 |
若 是第四象限角,
是第四象限角, ,则
,则
A.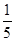 | B.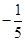 | C. | D. |
函数 的部分图象如图所示,则
的部分图象如图所示,则 的解析式为( )
的解析式为( )
A. |
B. |
C. |
D. |
 = ( )
= ( )
A. | B. | C.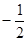 | D. |
若 ,则
,则 角的终边在
角的终边在
| A.第一、二象限 | B.第二、三象限 | C.第一、四象限 | D.第三、四象限 |