题目内容
在平面直角坐标系上，设不等式组
表示的平面区域为
，记内的整点（横坐标和纵坐标均为整数的点）的个数为
.
（1）求数列
的通项公式；
（2）若
，
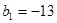.求证：数列
是等比数列，并求出数列
的通项公式.
【答案】
（1）
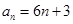；（2）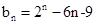
.
【解析】本试题主要是考查了数列的通项公式的求解和数列的概念和求和的综合运用。
解：（1）由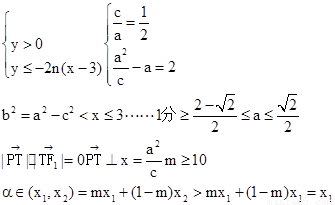
……………………………………1分
所以平面区域为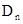
内的整点为点（3,0）或在直线
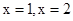上. …………2分
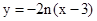直线
与直线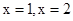交点纵坐标分别为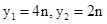
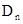内在直线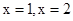上的整点个数分别为4n+1和2n+1, ……………4分
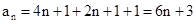…………………………………………5分
（2）由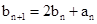
得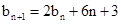
………………………………6分
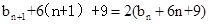………………………………………9分
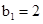……………………………………………………………10分
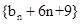是以2为首项，公比为2的等比数列……………………………11分
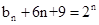……………………………………12分
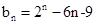……………………………13分
练习册系列答案
名校课堂系列答案
相关题目
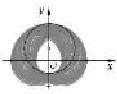如图，阴影是集合P={（x，y）|（x-cosθ）2+（y-sinθ）2=4，0≤θ≤π}在平面直角坐标系上表示的点集，则阴影中间形如“水滴”部分的面积等于（ ）A、π+
| ||||
B、
| ||||
C、
| ||||
| D、π+2 |
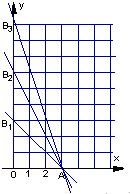在平面直角坐标系上，设不等式组