题目内容
在平面直角坐标系上,设不等式组
所表示的平面区域为Dn,记Dn内的整点(即横坐标和纵坐标均为整数的点)的个数为an(n∈N*).则a1=
|
6
6
,经推理可得到an=6n
6n
.分析:由题设知Dn内的整点在直线x=1或x=2或x=3上.记直线y=n(x-5)为l,l与两坐标轴围成的区域内,在直线x=1,x=2和x=3的点即为要找的整点,由a1=6,a2=12,a3=18,…归纳猜想得到an=6n(n∈N*).
解答:解:当n=1时,D1为直角三角形的内部包括斜边上,这时a1=6,
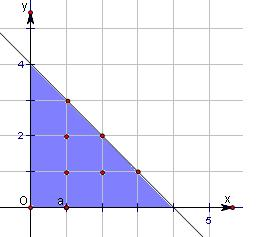
当n=2时,D2为直角三角形的内部包括斜边上,这时a2=12=2×6,
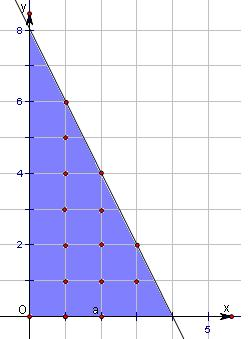
当n=3时,D3为直角三角形的内部包括斜边上,这时a3=18=3×6.
…
由此可猜想an=6n.
故答案为:6;6n.

当n=2时,D2为直角三角形的内部包括斜边上,这时a2=12=2×6,

当n=3时,D3为直角三角形的内部包括斜边上,这时a3=18=3×6.
…
由此可猜想an=6n.
故答案为:6;6n.
点评:本题考查归纳推理,数列的性质和应用,解题时要注意归纳猜想的合理运用.

练习册系列答案
相关题目
 如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )
如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )A、π+
| ||||
B、
| ||||
C、
| ||||
| D、π+2 |
 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组