题目内容
设数列 的前n项和为
的前n项和为 ,点
,点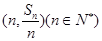 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设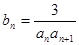 ,
,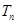 是数列
是数列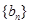 的前n项和,求使得
的前n项和,求使得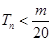 对所有
对所有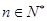 都成立的最小正整数m。
都成立的最小正整数m。
【答案】
(I) 。(II)满足要求的最小整数m为10。
。(II)满足要求的最小整数m为10。
【解析】本题考查数列与不等式的综合,综合性强,难度较大.易错点是基础知识不牢固,不会运用数列知识进行等价转化转化.解题时要认真审题,注意挖掘题设中的隐含条件.
1)设二次函数f(x)=ax2+bx.f'(x)=2ax+b,由2a=6b=-2,知f(x)=3x2-2x,由(n,Sn)在y=3x2-2x上,知Sn=3n2-2n.由此能求出数列{an}的通项公式.
(2)由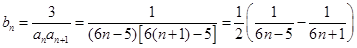 ,使得
,使得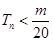 对所有
对所有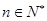 都成立,则m>20Tn恒成立.由此能求出所有n∈N*都成立的m的范围.
都成立,则m>20Tn恒成立.由此能求出所有n∈N*都成立的m的范围.
解:(I)依题意得,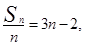 即
即 。
。
当n≥2时,a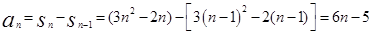 ;
;
当n=1时,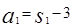 ×
×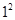 -2×1-1-6×1-5
-2×1-1-6×1-5
所以 。
。
(II)由(I)得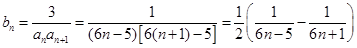 ,
,
故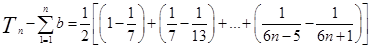 =
= 。
。
因此,使得 ﹤
﹤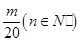 成立的m必须满足
成立的m必须满足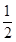 ≤
≤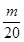 ,即m≥10,故满足要求的最小整数m为10。
,即m≥10,故满足要求的最小整数m为10。

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,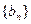 为等比数列,且
为等比数列,且 (Ⅰ)求数列
(Ⅰ)求数列 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.