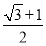Question

已知f(x)是以2为周期的偶函数，当x∈[0,1]时，f(x)＝，那么在区间(－1,3)内，关于x的方程f(x)＝kx＋k(k∈R)有4个根，则k的取值范围是(　　)．

A．0<k≤或k＝ B．0<k≤

C．0<k<或k＝ D．0<k<

 

Answer 1

B

【解析】因为直线y＝kx＋k过定点(－1,0)，画出函数f(x)在区间(－1,3)的图象，要使方程f(x)＝kx＋k(k∈R)有4个根，即直线y＝kx＋k和函数f(x)在区间(－1,3)的图象有4个交点，显然当0<k≤时满足条件，假若当直线y＝kx＋k和函数f(x)的图象在区间(2,3)上相切时也满足条件，但是这是不可能的，因为联立得ky2－y＋3k＝0，令Δ＝0得k＝或k＝－ (舍去)，当k＝时，解得x＝5∉(2,3)，所以0<k≤.，