题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 的解集包含
的解集包含![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1){x|x≤1,或x≥4};(2)[-3,0].
【解析】
试题分析:(1)当![]() 时,用分段函数的形式表示出函数
时,用分段函数的形式表示出函数![]() 的解析式,并分三种情况对其进行讨论,得出相应的不等式的解集,最后可得出该不等式的解集即可;(2)首先将问题
的解析式,并分三种情况对其进行讨论,得出相应的不等式的解集,最后可得出该不等式的解集即可;(2)首先将问题![]() 的解集包含
的解集包含![]() 转化为.当x∈[1,2]时,|x-4|-|x-2|≥|x+a|,进而转化为-2-a≤x≤2-a,由集合间的包含关系可得出证明.
转化为.当x∈[1,2]时,|x-4|-|x-2|≥|x+a|,进而转化为-2-a≤x≤2-a,由集合间的包含关系可得出证明.
试题解析:(1)当a=-3时,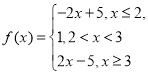
当x≤2时,由f(x)≥3得-2x+5≥3,解得x≤1;当2<x<3时,f(x)≥3无解;当x≥3时,由f(x)≥3得2x-5≥3,解得x≥4.所以f(x)≥3的解集为{x|x≤1,或x≥4}.
(2)f(x)≤|x-4||x-4|-|x-2|≥|x+a|.当x∈[1,2]时,|x-4|-|x-2|≥|x+a|4-x-(2-x)≥|x+a|-2-a≤x≤2-a.由条件得-2-a≤1且2-a≥2,即-3≤a≤0.故满足条件的a的取值范围是[-3,0].

练习册系列答案
相关题目