题目内容
 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准.为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准.为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:| 分组 | 频数 | 频率 |
| [0,1) | 25 | a |
| [1,2) | 38 38 |
0.19 |
| [2,3) | 50 | b |
| [3,4) | 46 46 |
0.23 |
| [4,5) | 36 36 |
0.18 |
| [5,6] | 5 | 0.025 0.025 |
(Ⅱ)若从样本中月均用水量在[5,6](单位:t)的5位居民中任选2人作进一步的调查研究,求月均用水量最多的居民被选中的频率(5位居民的月均用水量均不相等.)
分析:(I)从直方图中得在[2,3)小组中的频率,利用频率分布直方图中小长方形的面积=组距×
=频率求出b,再利用样本容量等于频数除以频率得出n,最后求出a处的数;
(II)设A,B,C,D,E代表用水量从多到少的5位居民,从中任选2为,总的基本事件为AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,包含A的有AB,AC,AD,AE共4个,根据古典概率计算公式计算即可.
| 频率 |
| 组距 |
(II)设A,B,C,D,E代表用水量从多到少的5位居民,从中任选2为,总的基本事件为AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,包含A的有AB,AC,AD,AE共4个,根据古典概率计算公式计算即可.
解答:解:(I)根据频率分布直方图中小长方形的面积=组距×
=频率,
从直方图中得在[2,3)小组中的频率为0.25×1=0.25,即b=0.25
从而n=
=200,
a=
=0.125.
∴n=200,a=0.125,b=0.25.
(II)设A,B,C,D,E代表用水量从多到少的5位居民,从中任选2为,总的基本事件为AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,包含A的有AB,AC,AD,AE共4个,
所以P=
=
.即为月均用水量最多的居民被选中的频率.
| 频率 |
| 组距 |
从直方图中得在[2,3)小组中的频率为0.25×1=0.25,即b=0.25
从而n=
| 50 |
| 0.25 |
a=
| 25 |
| 200 |
∴n=200,a=0.125,b=0.25.
(II)设A,B,C,D,E代表用水量从多到少的5位居民,从中任选2为,总的基本事件为AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,包含A的有AB,AC,AD,AE共4个,
所以P=
| 4 |
| 10 |
| 2 |
| 5 |
点评:用样本估计总体,是研究统计问题的一个基本思想方法.频率分布直方图中小长方形的面积=组距×
=频率,各个矩形面积之和等于1,能根据直方图求频率,属于常规题型.
| 频率 |
| 组距 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
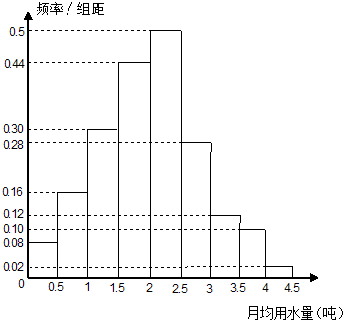 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量(单位:吨).根据所得的n个数据按照区间[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]进行分组,得到频率分布直方图如图
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量(单位:吨).根据所得的n个数据按照区间[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]进行分组,得到频率分布直方图如图

 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图 和
和 内的人数;
内的人数; )
)