题目内容
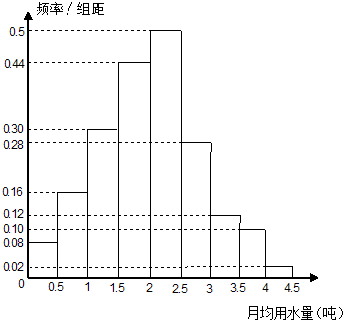
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
(I)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(II)用样本估计总体,如果希望80%的居民每月的用水量不超出标准&则月均用水量的最低标准定为多少吨,并说明理由;
(III)若将频率视为概率,现从该市某大型生活社区随机调查3位居民的月均用水量(看作有放回的抽样),其中月均用水量不超过(II)中最低标准的人数为x,求x的分布列和均值.

【答案】
(Ⅰ)见解析(Ⅱ)月均用水量的最低标准应定为2.5吨.(Ⅲ)
分布列为
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
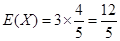
【解析】(Ⅰ)利用频率和为1可以补充频率分布直方图;(Ⅱ)根据频率分布直方图得到统计中的数值;(III)利用二项分布知识求出分布列和期望
(Ⅰ)
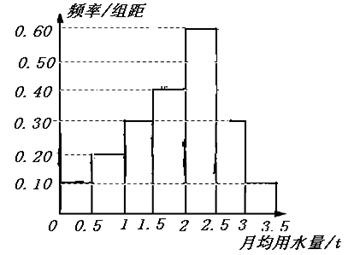
(Ⅱ)月均用水量的最低标准应定为2.5吨.样本中月均用水量不低于2.5吨的居民有20位,占样本总体的20%,由样本估计总体,要保证80%的居民每月的用水量不超出标准,月均用水量的最低标准应定为2.5吨.……………………………………………6分
(Ⅲ)依题意可知,居民月均用水量不超过(Ⅱ)中最低标准的概率是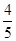 ,则
,则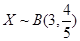 ,
,
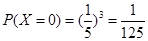
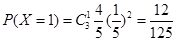
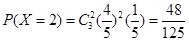
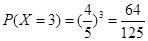 ………………8分
………………8分
分布列为
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
…………………………………………………………………………………………10分
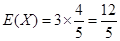

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
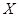


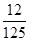

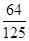
 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量(单位:吨).根据所得的n个数据按照区间[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]进行分组,得到频率分布直方图如图
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量(单位:吨).根据所得的n个数据按照区间[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]进行分组,得到频率分布直方图如图 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准.为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准.为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图 和
和 内的人数;
内的人数; )
)