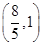题目内容
曲线![]() (θ为参数)上的点到两坐标轴的距离之和的最大值是( )
(θ为参数)上的点到两坐标轴的距离之和的最大值是( )
A.![]() B.
B.![]() C.1 D.2
C.1 D.2
D
解析:
解法一:因为曲线方程可化为x2+y2=1,所以曲线是圆心在原点,半径为1的圆.那么圆上任一点到两坐标轴的距离之和必不小于1,也不会恒等于1.(这是因为直角三角形两直角边之和大于斜边),即最大值必大于1.故选D.
解法二:当θ=![]() 时,点(cosθ,sinθ)为(
时,点(cosθ,sinθ)为(![]() ,
,![]() ),到两坐标轴距离之和是
),到两坐标轴距离之和是![]() +
+![]() =
=![]() >1,故所求的最大值不小于1.故选D.
>1,故所求的最大值不小于1.故选D.
解法三:曲线上的点到两坐标距离之和d满足d2=(|sinθ|+|cosθ|)2=1+|sin2θ|≤1+1=2.
当且仅当|sin2θ|=1时取等号,∴d≤![]() .故选D.
.故选D.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
在曲线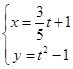 (
(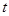 为参数)上的点是( )
为参数)上的点是( )
A.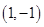 | B.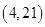 | C.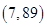 | D.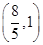 |
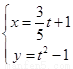 (
(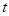 为参数)上的点是( )
为参数)上的点是( )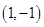 B.
B.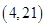 C.
C.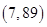 D.
D. 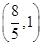
 (
( 为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移
为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移 个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线
个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线 .以坐标原点为极点,
.以坐标原点为极点, 的非负半轴为极轴,建立的极坐标中的曲线
的非负半轴为极轴,建立的极坐标中的曲线 的方程为
的方程为 ,求
,求 和
和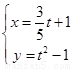 (
(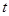 为参数)上的点是( )
为参数)上的点是( )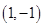 B.
B. C.
C. D.
D.