题目内容
 = ,
= , = .
= .
【答案】分析:欲求k的值,只须求出函数3x2+k的定积分值即可,故先利用导数求出3x2+k的原函数,再结合积分定理即可求出用k表示的定积分.最后列出等式即可求得k值,求出函数 的原函数,根据定积分的公式进行求解即可.
的原函数,根据定积分的公式进行求解即可.
解答:解:∵∫2(3x2+k)dx
=(x3+kx)|2
=23+2k.
由题意得:
23+2k=10,
∴k=1.
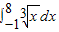 =
=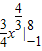 =
=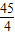
故答案为:1,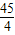 .
.
点评:本小题主要考查直定积分的简单应用、定积分、利用导数研究原函数等基础知识,考查运算求解能力,属于基础题.
 的原函数,根据定积分的公式进行求解即可.
的原函数,根据定积分的公式进行求解即可.解答:解:∵∫2(3x2+k)dx
=(x3+kx)|2
=23+2k.
由题意得:
23+2k=10,
∴k=1.
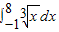 =
=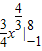 =
=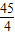
故答案为:1,
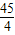 .
.点评:本小题主要考查直定积分的简单应用、定积分、利用导数研究原函数等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
一个容量100的样本,其数据的分组与各组的频数如下表
则样本数据落在(10,40)上的频率为( )
A.0.13
B.0.39
C.0.52
D.0.64
| 组别 | (0,10] | (10,20] | (20,30) | (30,40) | (40,50] | (50,60] | (60,70] |
| 频数 | 12 | 13 | 24 | 15 | 16 | 13 | 7 |
A.0.13
B.0.39
C.0.52
D.0.64
 ,
,
 ,
,
 ,y=x+3
,y=x+3
 .
.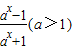 .
.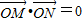 (其中O为坐标原点)求m的值;
(其中O为坐标原点)求m的值;


