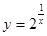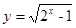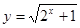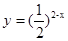题目内容
定义在R上的函数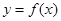 是减函数,且函数
是减函数,且函数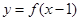 的图象关于(1,0)成中心对称,若实数
的图象关于(1,0)成中心对称,若实数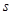 满足不等式
满足不等式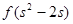 +
+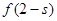
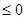 ,则
,则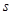 的取值范围是___________.
的取值范围是___________.
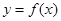 是减函数,且函数
是减函数,且函数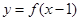 的图象关于(1,0)成中心对称,若实数
的图象关于(1,0)成中心对称,若实数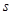 满足不等式
满足不等式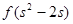 +
+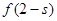
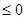 ,则
,则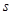 的取值范围是___________.
的取值范围是___________.(-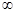 ,1]∪[2,
,1]∪[2,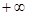 )
)
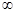 ,1]∪[2,
,1]∪[2,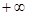 )
)试题分析:因为函数
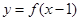 的图象关于(1,0)成中心对称,所以函数
的图象关于(1,0)成中心对称,所以函数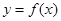 的图象关于坐标原点对称,所以函数
的图象关于坐标原点对称,所以函数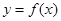 是奇函数,且是R上的减函数,所以由
是奇函数,且是R上的减函数,所以由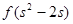 +
+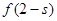
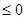 可得
可得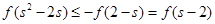 ,所以
,所以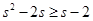 ,所以
,所以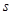 的取值范围是(-
的取值范围是(-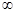 ,1]∪[2,
,1]∪[2,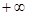 ).
).点评:解决本小题的关键是准确转化问题条件,灵活运算函数的性质.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 .
. 的单调递增区间;
的单调递增区间;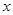 的方程
的方程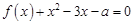 在区间
在区间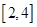 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数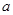 的取值范围.
的取值范围.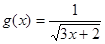 的定义域为 。
的定义域为 。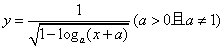 的定义域.
的定义域.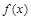 ,当
,当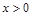 时,
时,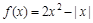 ,则
,则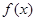 在
在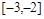 上是( )
上是( )
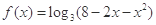 ,设其定义域域是
,设其定义域域是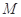 .
.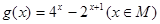 的值域.
的值域.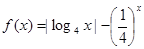 的零点分别为
的零点分别为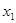 ,
,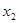 ,则( )
,则( )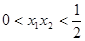

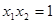
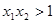
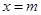 和
和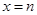 是函数
是函数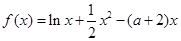 的两个极
的两个极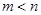 ,
,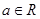 .(Ⅰ) 求
.(Ⅰ) 求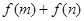 的取值范围;
的取值范围;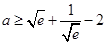 ,求
,求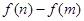 的最大值.
的最大值.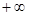 )的函数是( )
)的函数是( )