题目内容
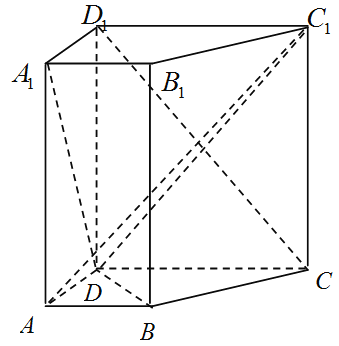
【题目】如图，在直四棱柱
中，已知
，
．
（1）求证：
；
（2）设
是
上一点，试确定的位置，使
平面
，并说明理由．
【答案】⑴连DC1,正方形DD1C1C中,D1C⊥C1D
∵AD⊥平面DD1C1C ∴AD⊥CD1又AD∩CD1=D
∴CD1⊥平面DA C1
⑵ E 为AC中点时，
平面
9’
梯形ABCD中，DE∥且=" AB " ∴AD∥且=BE
∵AD∥且= A1D1∴A1D1∥且="BE " ∴A1D1EB是平行四边形
∴D1E∥B A1又B A1
平面DB A1D1E
平面DB A1
∴平面
【解析】试题分析：
（1）本题为证线与线垂直，常规思路为转化为证线与另一条
直线所在的平面垂直。结合条件，可证出
平面
，则得：.
（2）本题为通过确定点
的位置来证明证线与面平行，可通过题中的条件进行大胆设想，（为中点），然后进行对应的证明，可解决；
试题解析：
（1）在直四棱柱
中，
连结
，
，
四边形
是正方形．
．
又
，
，
平面，
平面，
．
平面，且
，
平面，又
平面，
．
（2）连结
，连结
，设
，
，连结
，
平面
平面
，
要使平面，须使
，
又
是的中点．
是的中点．
又易知
，
．
即是
的中点．综上所述，当是的中点时，可使平面．
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关，通过随机抽查110名学生，得到如下2×2的列联表：
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式K2= 
，算得K2≈7.61
附表：
p（K2≥k0） | 0.025 | 0.01 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
参照附表，以下结论正确是（ ）
A.有99.5%以上的把握认为“爱好该项运动与性别有关”
B.有99.5%以上的把握认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
