题目内容
(本小题10分)
如图,已知AP是 O的切线,P为切点,AC是
O的切线,P为切点,AC是 O的割线,与
O的割线,与 O交于B,C两点,圆心O在
O交于B,C两点,圆心O在 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。

(1) 证明:A,P,O,M四点共圆;
(2)
求 OAM+
OAM+ APM的大小。
APM的大小。
【答案】
(本小题10分)
(1)证明:如图,连结OP,OM.
∵AP与 O相切于点P,∴OP⊥AP.
O相切于点P,∴OP⊥AP.
∵点M是 O 的弦BC的中点,∴OM⊥BC。
O 的弦BC的中点,∴OM⊥BC。
于是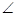 OPA+
OPA+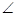 OMA=180°
OMA=180°
即四边形APOM的对角互补
∴A,P,O,M四点共圆
(2)由(1)得A,P,O,M四点共圆
∴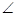 OAM=
OAM=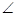 OPM。
OPM。
由(1)得OP⊥AP,由圆心O在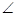 PAC的内部,可知
PAC的内部,可知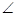 OPM+
OPM+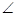 APM=90°
APM=90°
所以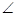 OAM+
OAM+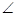 APM=90°。
APM=90°。
【解析】

练习册系列答案
相关题目

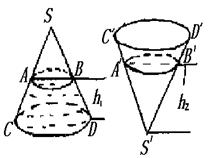
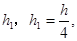 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为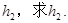
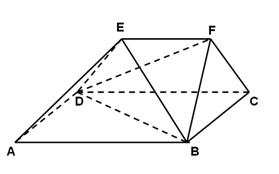
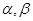 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为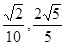
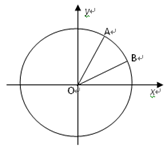
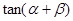 的值; (2)求
的值; (2)求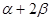 的值。
的值。