题目内容
设函数
(Ⅰ)当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)若当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
【答案】
(1)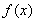 的单增区间为
的单增区间为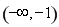 ,
,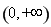 ;单减区间为
;单减区间为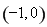 ;(2)
;(2)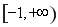 .
.
【解析】
试题分析:本题主要考查导数的运算以及利用导数研究函数的单调性和最值以及恒成立问题,考查函数思想,分类讨论思想,考查综合分析和解决问题的能力.第一问,将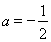 代入得到具体的函数解析式,利用
代入得到具体的函数解析式,利用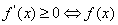 为增函数,
为增函数,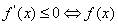 为减函数,解不等式求出函数的单调区间;第二问,化简
为减函数,解不等式求出函数的单调区间;第二问,化简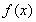 解析式,由于
解析式,由于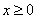 ,所以只需
,所以只需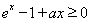 恒成立即可,所以设出新函数
恒成立即可,所以设出新函数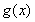 ,求导,判断
,求导,判断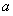 的取值范围,求出函数
的取值范围,求出函数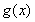 的最小值,令最小值大于等于0,判断符合题意的
的最小值,令最小值大于等于0,判断符合题意的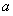 的取值范围.
的取值范围.
试题解析:(1)当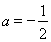 时,
时,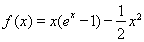 ,
,
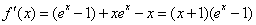 2分
2分
令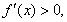 得
得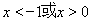 ;令
;令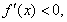 得
得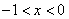
所以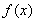 的单增区间为
的单增区间为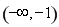 ,
,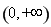 ;单减区间为
;单减区间为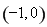 5分
5分
(2)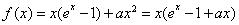 ,令
,令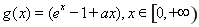 ,
,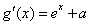 ,
, 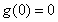 7分
7分
当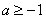 时,
时,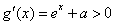 ,
,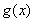 在
在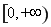 上为增函数,而
上为增函数,而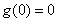 ,从而当
,从而当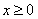 时,
时,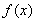
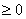 恒成立. 9分
恒成立. 9分
当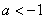 时,令
时,令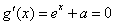 ,得
,得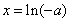 .当
.当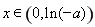 时,
时,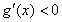 ,
,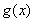 在
在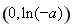 上是减函数,而
上是减函数,而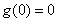 ,从而当
,从而当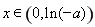 时,
时,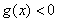 ,即
,即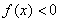
综上,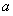 的取值范围是
的取值范围是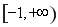 12分
12分
考点:1.利用导数研究函数的单调性;2.恒成立问题;3.利用导数研究函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
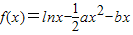 .
.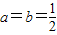 时,求f(x)的最大值;
时,求f(x)的最大值;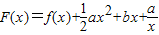 ,(0<x≤3),其图象上任意一点P(x,y)处切线的斜率k≤
,(0<x≤3),其图象上任意一点P(x,y)处切线的斜率k≤ 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;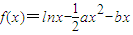 .
.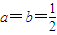 时,求f(x)的最大值;
时,求f(x)的最大值;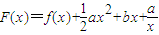 ,(0<x≤3),其图象上任意一点P(x,y)处切线的斜率k≤
,(0<x≤3),其图象上任意一点P(x,y)处切线的斜率k≤ 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;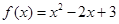
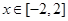 时,求
时,求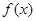 的值域
的值域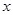 的不等式:
的不等式: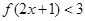
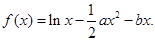 (1)当
(1)当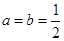 时,求
时,求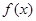 的最大值;(2)令
的最大值;(2)令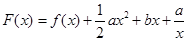 ,(
,(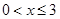 ),其图象上任意一点
),其图象上任意一点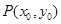 处切线的斜率
处切线的斜率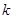 ≤
≤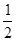 恒成立,求实数
恒成立,求实数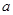 的取值范围;(3)当
的取值范围;(3)当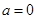 ,
,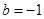 ,方程
,方程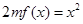 有唯一实数解,求正数
有唯一实数解,求正数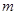 的值.
的值.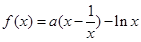
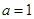 时,求曲线
时,求曲线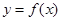 在点
在点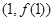 处的切线方程;
处的切线方程;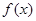 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数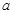 的取值范围;
的取值范围;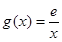 ,若在
,若在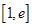 上至少存在一点
上至少存在一点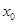 使
使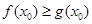 成立,求实数
成立,求实数