题目内容
7．已知函数f（x）$\left\{\begin{array}{l}{x-2，x≥2}\\{\frac{1}{2}x-1，x＜2}\end{array}\right.$的图象与函数f（x）=log3x的图象的交点个数是2．分析 令g（x）=log3x，在同一坐标系内画出函数f（x），g（x）图象，数形结合可得答案．
解答 解：令g（x）=log3x，
在同一坐标系内画出函数f（x），g（x）图象如图所示：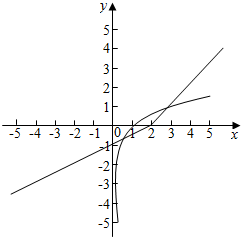
由图可得：函数f（x），g（x）图象共有2个交点，
即函数f（x）=log3x的图象的交点个数为2个，
故答案为：2．
点评 本题考查的知识点是分段函数的应用，函数的零点，难度中档．
练习册系列答案
相关题目
18．设函数f（x）=x2+3x-5lnx，则f（x）的递减区间为（ ）
| A． | （-$\frac{5}{2}$，1） | B． | （-∞，-$\frac{5}{2}$），（1，+∞） | C． | （1，+∞） | D． | （0，1） |
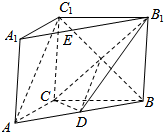如图，在直三棱柱ABC-A1B1C1中，AC=BC=2，AB=2$\sqrt{3}$，AA1=2，点D是AB的中点．