题目内容
下面有5个命题:①函数y=sin4x-cos4x的最小正周期是π.
②终边在y轴上的角的集合是{α|α=
| kπ |
| 2 |
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④函数y=sin(2x+
| π |
| 3 |
| π |
| 12 |
⑤函数y=sin(x-
| π |
| 2 |
其中,真命题的编号是
分析:根据二倍角的余弦公式,平方差公式,同角三角形函数平方关系,化简解析式,再由余弦函数的周期性,可以判断①的真假;由终边相同的角的集合表示法,可以判断②的真假;根据正弦函数的图象和性质,可以判断③的真假;根据函数图象的平移变换法则,可以判断④的真假;根据诱导公式,将函数化为余弦型,进而根据余弦函数的单调性,可以判断⑤的真假;进而得到答案.
解答:解:函数y=sin4x-cos4x=(sin2x+cos•x)•(sin2x-cos2x)=-cos2x的最小正周期是π,故①正确;
终边在y轴上的角的集合是{α|α=
+kπ,k∈Z},故②错误;
在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点,故③错误;
函数y=sin(2x+
)图象的对称轴方程是x=
+
π,k∈Z,当k=0时,x=
,故④正确;
函数y=sin(x-
)=-cosx在[0,π]上是增函数,故⑤错误
故答案为:①④
终边在y轴上的角的集合是{α|α=
| π |
| 2 |
在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点,故③错误;
函数y=sin(2x+
| π |
| 3 |
| π |
| 12 |
| k |
| 2 |
| π |
| 12 |
函数y=sin(x-
| π |
| 2 |
故答案为:①④
点评:本题考查的知识点是命题的真假判断及其应用,余弦型函数的周期性,终边相同的角,正弦函数的性质,图象的平移变换,及三角函数的单调性,熟练掌握上述基础知识,并判断出题目中4个命题的真假,是解答本题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
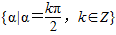 .③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.④函数
.③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.④函数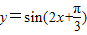 图象的对称轴方程可能是
图象的对称轴方程可能是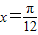 .⑤函数
.⑤函数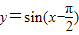 在[0,π]上是减函数.其中,真命题的编号是 (写出所有真命题的编号)
在[0,π]上是减函数.其中,真命题的编号是 (写出所有真命题的编号)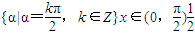
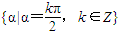 ;
;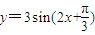 的图象向右平移
的图象向右平移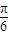 得到y=3sin2x的图象;
得到y=3sin2x的图象;