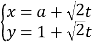题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
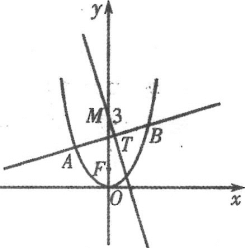
(2)若直线![]() 与
与![]() 相切于第二象限的点
相切于第二象限的点![]() ,与
,与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接消去参数,把参数方程化成普通方程,利用互化公式,将极坐标方程转换成直角坐标方程;
(2)设![]() 的倾斜角为
的倾斜角为![]() ,
,![]() ,写出直线
,写出直线![]() 参数方程,代入
参数方程,代入![]() :
:![]() ,得出关于
,得出关于![]() 的一元二次方程,写出韦达定理,利用直线参数方程中参数的几何意义和三角函数关系式的恒等变换求出结果.
的一元二次方程,写出韦达定理,利用直线参数方程中参数的几何意义和三角函数关系式的恒等变换求出结果.
(1)因为![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
所以![]() 的普通方程为:
的普通方程为:![]() .
.
因为![]() 的极坐标方程为
的极坐标方程为![]() ,
,
由![]() ,
,![]() ,
,
得![]() 的直角坐标方程为:
的直角坐标方程为:![]() .
.
(2)如图,设![]() 的倾斜角为
的倾斜角为![]() ,依题意
,依题意![]() ,
,
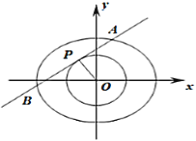
则![]() 在
在![]() 中的参数角
中的参数角![]() ,故
,故![]() ,
,
所以可设![]() 的参数方程
的参数方程![]() (
(![]() 为参数).
为参数).
把![]() 的参数方程代入
的参数方程代入![]() ,
,
得![]() ,
,
所以![]() .
.
则 ,
,
又![]() ,所以
,所以![]() ,解得:
,解得:![]() ,
,
故![]() ;即直线
;即直线![]() 的倾斜角为
的倾斜角为![]() .
.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
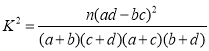 (其中
(其中![]() ).
).
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
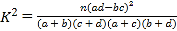 (其中
(其中![]() ).
).