题目内容
已知偶函数 满足:当
满足:当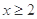 时,
时, ,当
,当 时,
时,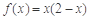 .
.
(1)求当 时,
时, 的表达式;
的表达式;
(2)试讨论:当实数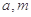 满足什么条件时,函数
满足什么条件时,函数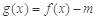 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
【答案】
(1) ;(2)①
;(2)① 时,
时, ;②
;② 时,
时, ;③
;③ 时,
时, .
.
【解析】
试题分析:本题考查函数的奇偶性、函数解析式、函数零点问题以及等差数列的定义,考查化归与转化思想,考查计算能力.第一问,先把 转化成
转化成 ,利用已知
,利用已知 时的解析式,利用偶函数转化解析式;第二问,把
时的解析式,利用偶函数转化解析式;第二问,把 有4个零点,先转化为
有4个零点,先转化为 与
与 有4个交点且均匀分布,所以利用等差中项,偶函数等基础知识列出表达式,分情况进行讨论分析.
有4个交点且均匀分布,所以利用等差中项,偶函数等基础知识列出表达式,分情况进行讨论分析.
试题解析:(1)设 则
则 ,
, ,
,
又
 偶函数
偶函数 ,
,
所以, .
.
(2) 零点
零点 ,
, 与
与 交点有4个且均匀分布,
交点有4个且均匀分布,
(Ⅰ) 时,
时,
 得
得 ,
,
所以 时,
时, ,
,
(Ⅱ) 且
且 时
,
时
, ,
,
 ,
,
所以  时,
时, ,
,
(Ⅲ) 时
时 时,符合题意,
时,符合题意,
(Ⅳ) 时,
时, ,
, ,
, ,
, ,
,
此时, ,所以
,所以 或
或 (舍)
(舍)
 且
且 时,
时, 时存在.
时存在.
综上,① 时,
时, ;
;
② 时,
时, ;
;
③ 时,
时, 符合题意.
符合题意.
考点:1.求函数解析式;2.函数零点问题;3.图像交点问题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
. 表达式;
表达式; 与函数
与函数 的取值范围;
的取值范围;  满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 上.(不要求过程)
上.(不要求过程) 满足:当
满足:当 时,
时, ,
,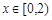 时,
时,
 时,
时, 的表达式;
的表达式; 满足什么条件时,函数
满足什么条件时,函数 有4个零点,
有4个零点, 满足:当
满足:当 时,
时, ,当
,当 时,
时,
 时,
时, 的表达式;
的表达式; 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。 满足:当
满足:当 时,
时,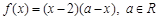 ,当
,当 时,
时,
 时,
时, 的表达式;
的表达式; 与函数
与函数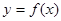 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。