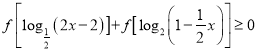Question

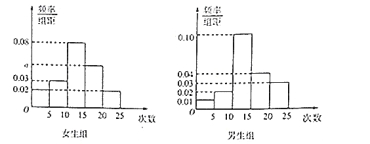
【题目】某中学为了了解全校学生的上网情况，在全校采用随机抽样的方法抽取了40名学生（其中男女生人数恰好各占一半）进行问卷调查，并进行了统计，按男女分为两组，再将每组学生的月上网次数分为5组：，，，，，得到如图所示的频率分布直方图：

（1）写出的值；

（2）求抽取的40名学生中月上网次数不少于15次的学生人数；

（Ⅲ）在抽取的40名学生中，从月上网次数不少于20次的学生中随机抽取2人 ，求至少抽到1名女生的概率.

Answer 1

【答案】（1）0.05；

（2）抽取的40名学生中月上网次数不少于15次的学生人数有7+7=14人；

（Ⅲ）.

【解析】

试题分析：（1）直接由频率分布直方图即可计算出的值即可；（2）首先求出在抽取的女生中，月上网次数不少于20次的学生频率和学生人数和在抽取的男生中，月上网次数不少于20次的学生频率和学生人数，然后求出在所抽取的男生中，月上网次数不少于15次的学生即可；（3）首先记“在抽取的40名学生中，从月上网次数不少于20次的学生中随机抽取2人，至少抽到1名女生”为事件，然后分别求出在抽取的女生和男生中，月上网次数不少于20次的学生频率和人数，记这2名女生为，，这3名男生为，，，并列举各自的可能种数，最后由古典概型的计算公式即可得出所求的结果.

试题解析：（1）.

（2）在所抽取的女生中，月上网次数不少于15次的学生频率为（0.05+0.02）×5=0.35，所以，在所抽取的女生中，月上网次数不少于15次的学生有0.03×20=7人.

在所抽取的男生中，月上网次数不少于15次的学生频率为（0.04+0.03）×5=0.35，所以，在所抽取的男生中，月上网次数不少于15次的学生有0.03×20=7人.

故抽取的40名学生中月上网次数不少于15次的学生人数有7+7=14人.

（Ⅲ）记“在抽取的40名学生中，从月上网次数不少于20次的学生中随机抽取2人，至少抽到1名女生”为事件，在抽取的女生中，月上网次数不少于20次的学生频率为0.02×5=0.1，人数为0.1×20=2人，

在抽取的男生中，月上网次数不少于20次的学生频率为0.03×5=0.15，人数为0.15×20=3人，

记这2名女生为，，这3名男生为，，，

则在抽取的40名学生中，从月上网次数不少于20次的学生中随机抽取2人，所有可能结果有10种，即，，，，，，，，，，

而事件包含的结果有7种，它们是，，，，，，，

所以.