题目内容
9. 如图,在边长为4 的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE
如图,在边长为4 的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC,如图.
(1)求证:A1E⊥平面BCDE;
(2)求二面角E-A1B-C的余弦值;
(3)判断在线段EB上是否存在一点P,使平面A1DP⊥平面A1BC?若存在,求出$\frac{EP}{PB}$的值;若不存在,说明理由.
分析 (1)证明DC⊥平面A1DE,可得DC⊥A1E,利用A1E⊥DE,DC∩DE=D,可得A1E⊥平面BCDE;
(2)以EB,ED,EA1分别为x,y,z轴,建立坐标系,求出平面A1BE、平面A1BC的一个法向量,利用向量的夹角公式求二面角E-A1B-C的余弦值;
(3)设P(t,0,0)(0≤t≤2),求出平面A1DP的法向量,利用平面A1DP⊥平面A1BC,可得结论.
解答 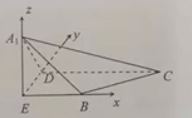 (1)证明:∵DE⊥BE,BE∥DC,
(1)证明:∵DE⊥BE,BE∥DC,
∴DE⊥DC,
∵A1D⊥DC,A1D∩DE=D,
∴DC⊥平面A1DE,
∴DC⊥A1E,
∵A1E⊥DE,DC∩DE=D,
∴A1E⊥平面BCDE;
(2)解:由题意,以EB,ED,EA1分别为x,y,z轴,建立坐标系,则DE=2$\sqrt{3}$,
A1(0,0,2),B(2,0,0),C(4,2$\sqrt{3}$,0),D(0,2$\sqrt{3}$,0),
∴$\overrightarrow{B{A}_{1}}$=(-2,0,2),$\overrightarrow{BC}$=(2,2$\sqrt{3}$,0),
平面A1BE的一个法向量为$\overrightarrow{n}$=(0,1,0),
设平面A1BC的一个法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{-2x+2z=0}\\{2x+2\sqrt{3}y=0}\end{array}\right.$,
∴$\overrightarrow{m}$=(-$\sqrt{3}$,1,-$\sqrt{3}$),
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\sqrt{7}}{7}$,
∴二面角E-A1B-C的余弦值为-$\frac{\sqrt{7}}{7}$;
(3)解:在线段EB上不存在一点P,使平面A1DP⊥平面A1BC,
设P(t,0,0)(0≤t≤2),则$\overrightarrow{{A}_{1}P}$=(t,0,-2),$\overrightarrow{{A}_{1}D}$=(0,2$\sqrt{3}$,-2),
设平面A1DP的法向量为$\overrightarrow{p}$=(a,b,c),则$\left\{\begin{array}{l}{2\sqrt{3}b-2c=0}\\{ta-2c=0}\end{array}\right.$,
∴$\overrightarrow{p}$=(2,$\frac{t}{\sqrt{3}}$,t),
∵平面A1DP⊥平面A1BC,
∴-2$\sqrt{3}$+$\frac{t}{\sqrt{3}}$-$\sqrt{3}$t=0,
∴t=-3,
∵0≤t≤2,
∴在线段EB上不存在一点P,使平面A1DP⊥平面A1BC.
点评 本题考查线面垂直的判定与性质,考查二面角的计算,考查平面与平面垂直,正确运用向量法,求出平面的法向量是关键.

| 年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 人数 | 4 | 5 | 8 | 5 | 3 |
| 年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
| 人数 | 6 | 7 | 3 | 5 | 4 |
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都是赞成的概率;
(Ⅱ)求选中的4人中,至少有3人赞成的概率;
(Ⅲ)若选中的4人中,不赞成的人数为X,求随机变量X的分布列和数学期望.
| A. | 2+i | B. | 1+2i | C. | 1-2i | D. | 2-i |
| A. | 30 | B. | 45 | C. | 63 | D. | 84 |