题目内容
若x,y满足:x+y-3≥0,x-y+1=0,3x-y-5≤0,设y=kx,则k的取值范围是分析:本题考查的是线性规划问题,首先要根据线性约束条件画出可行域,然后根据目标函数借助于斜率的几何意义,找到临界状态,从而找到k的取值范围.
解答: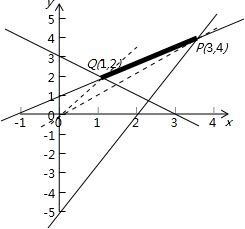 解:由线性约束条件可画图如下:
解:由线性约束条件可画图如下:
由目标函数y=kx可知,k=
.
故k的取值即过原点和线段PQ上的点直线斜率的取值,
又由
知P点的坐标为(3,4),
由
知Q点的坐标为(1,2).
所以kOP≤k≤kOQ,即
≤k≤2.
故k的取值范围是[
,2].
 解:由线性约束条件可画图如下:
解:由线性约束条件可画图如下:由目标函数y=kx可知,k=
| y |
| x |
故k的取值即过原点和线段PQ上的点直线斜率的取值,
又由
|
由
|
所以kOP≤k≤kOQ,即
| 4 |
| 3 |
故k的取值范围是[
| 4 |
| 3 |
点评:此题考查了线性规划的基本内容,比如由线性约束条件画可行域、变形目标函数以及根据目标函数的形式应用其几何意义进一步分析问题转化问题的思维规律值得反思和总结.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
已知向量
=(x+z,3),
=(2,y-z),且
⊥
,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )
| a |
| b |
| a |
| b |
| A、[-2,2] |
| B、[-2,3] |
| C、[-3,2] |
| D、[-3,3] |