题目内容
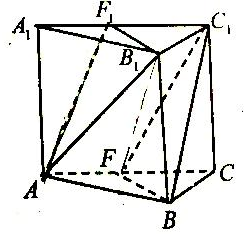
如图,在正三棱柱ABC-A1B1C1中,F、F1分别是AC、A1C1的中点
(1)求证:平面AB1F∥平面C1BF;
(2)若BC=2,CC1=2
,求异面直线AF1和BC1所成角的正弦值.
(1)求证:平面AB1F∥平面C1BF;
(2)若BC=2,CC1=2
| 3 |

考点:异面直线及其所成的角,平面与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)直接根据已知条件求出相交直线平行与相交直线,得到面面平行.
(2)首先求出异面直线的夹角,进一步利用余弦定理求出结果,最后转化成正弦值.
(2)首先求出异面直线的夹角,进一步利用余弦定理求出结果,最后转化成正弦值.
解答:
(1)证明:在正三棱柱ABC-A1B1C1中,F、F1分别是AC、A1C1的中点,
所以:BF∥B1F1,AF1∥C1F
所以:平面AB1F∥平面C1BF.
(2)解:在正三棱锥中,BF∥B1F1,异面直线AF1和BC1所成角
即:直线C1F和BC1所成角.
利用关系式求得:BF=
,
BC1=C1F=4
利用余弦定理求得:cos∠BC1F=
=
sin∠BC1F=
所以:BF∥B1F1,AF1∥C1F
所以:平面AB1F∥平面C1BF.
(2)解:在正三棱锥中,BF∥B1F1,异面直线AF1和BC1所成角
即:直线C1F和BC1所成角.
利用关系式求得:BF=
| 3 |
BC1=C1F=4
利用余弦定理求得:cos∠BC1F=
| BC12+C1F2-BF2 |
| 2BC1•C1F |
| 29 |
| 32 |
sin∠BC1F=
| ||
| 32 |
点评:本题考查的知识要点:面面平行的判定定理,异面直线的夹角及相关的运算.属于基础题型.

练习册系列答案
相关题目
从装有大小相同的3个红球和2个白球的口袋内任取1个球,取到白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图:已知在?ABCD中,对角线AC交BD于O、E为DO的中点,AE交CD于F,设
=
,
=
,则
=( )

| AB |
| a |
| AD |
| b |
| BF |

A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|