题目内容
已知A(3,1),抛物线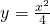 上一点P(x,y),则|PA|+y的最小值为 ________.
上一点P(x,y),则|PA|+y的最小值为 ________.
2
分析:先根据抛物线方程求得准线方程和焦点坐标,记P在直线y=-1上的射影为Q,进而可知y=|PQ|-1=|PF|-1,根据抛物线的定义可把问题转化为求|PA|+|PF|的最小值,进而利用数形结合的方法可知当且既当F、P、A共线时有最小值,答案可得.
解答:抛物线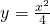 的准线为:y=-1,焦点F(0,1),
的准线为:y=-1,焦点F(0,1),
记P在直线y=-1上的射影为Q,
则y=|PQ|-1=|PF|-1,|PA|+y=|PA|+|PF|-1,
问题转化为:求|PA|+|PF|的最小值,易见:|PA|+|PF|≥|AF|=3,
当且既当F、P、A共线时等号成立,
故:|PA|+y的最小值为2.
故答案为:2
点评:本题主要考查了抛物线的简单性质,特别是抛物线定义的运用.考查了学生运用数形结合的方法解决数学问题的能力.
分析:先根据抛物线方程求得准线方程和焦点坐标,记P在直线y=-1上的射影为Q,进而可知y=|PQ|-1=|PF|-1,根据抛物线的定义可把问题转化为求|PA|+|PF|的最小值,进而利用数形结合的方法可知当且既当F、P、A共线时有最小值,答案可得.
解答:抛物线
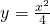 的准线为:y=-1,焦点F(0,1),
的准线为:y=-1,焦点F(0,1),记P在直线y=-1上的射影为Q,
则y=|PQ|-1=|PF|-1,|PA|+y=|PA|+|PF|-1,
问题转化为:求|PA|+|PF|的最小值,易见:|PA|+|PF|≥|AF|=3,
当且既当F、P、A共线时等号成立,
故:|PA|+y的最小值为2.
故答案为:2
点评:本题主要考查了抛物线的简单性质,特别是抛物线定义的运用.考查了学生运用数形结合的方法解决数学问题的能力.

练习册系列答案
相关题目
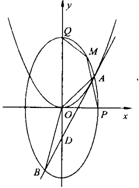 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.