题目内容
已知 ,若存在区间[a,b]⊆(0,+∞),使得{y|y=f(x),x∈[a,b]}=[ma,mb],则实数m的取值范围是 .
,若存在区间[a,b]⊆(0,+∞),使得{y|y=f(x),x∈[a,b]}=[ma,mb],则实数m的取值范围是 .
【答案】分析:依题意,f(x)=4-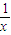 在[a,b]上单调增,则f(a)=ma,f(b)=mb,从而可得mx2-x+1=0必须有两个不相等的正根,利用该方程有二异正根的条件即可求得实数m的取值范围.
在[a,b]上单调增,则f(a)=ma,f(b)=mb,从而可得mx2-x+1=0必须有两个不相等的正根,利用该方程有二异正根的条件即可求得实数m的取值范围.
解答:解:∵f(x)=4-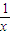 在(0,+∞)是增函数,
在(0,+∞)是增函数,
∴f(x)在x∈[a,b]上值域为[f(a),f(b)]
所以f(a)=ma且f(b)=mb,
即4-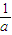 =ma且4-
=ma且4-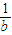 =mb,
=mb,
所以ma2-4a+1=0且mb2-4b+1=0,
所以mx2-4x+1=0必须有两个不相等的正根,故m≠0,
∴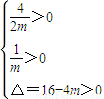 ,解得0<m<4.
,解得0<m<4.
∴实数m的取值范围是(0,4).
故答案为:(0,4).
点评:本题考查函数单调性的性质,着重考查二次函数根的分布问题,将所求的问题转化为mx2-x+1=0必须有两个不相等的正根是关键,属于难题.
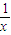 在[a,b]上单调增,则f(a)=ma,f(b)=mb,从而可得mx2-x+1=0必须有两个不相等的正根,利用该方程有二异正根的条件即可求得实数m的取值范围.
在[a,b]上单调增,则f(a)=ma,f(b)=mb,从而可得mx2-x+1=0必须有两个不相等的正根,利用该方程有二异正根的条件即可求得实数m的取值范围.解答:解:∵f(x)=4-
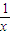 在(0,+∞)是增函数,
在(0,+∞)是增函数,∴f(x)在x∈[a,b]上值域为[f(a),f(b)]
所以f(a)=ma且f(b)=mb,
即4-
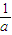 =ma且4-
=ma且4-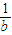 =mb,
=mb,所以ma2-4a+1=0且mb2-4b+1=0,
所以mx2-4x+1=0必须有两个不相等的正根,故m≠0,
∴
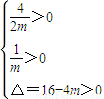 ,解得0<m<4.
,解得0<m<4.∴实数m的取值范围是(0,4).
故答案为:(0,4).
点评:本题考查函数单调性的性质,着重考查二次函数根的分布问题,将所求的问题转化为mx2-x+1=0必须有两个不相等的正根是关键,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
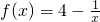 ,若存在区间[a,b]⊆(0,+∞),使得{y|y=f(x),x∈[a,b]}=[ma,mb],则实数m的取值范围是________.
,若存在区间[a,b]⊆(0,+∞),使得{y|y=f(x),x∈[a,b]}=[ma,mb],则实数m的取值范围是________. ,若存在区间
,若存在区间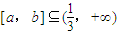 ,使得{y|y=f(x),x⊆[a,b]}=[ma,mb],则实数m的取值范围是 .
,使得{y|y=f(x),x⊆[a,b]}=[ma,mb],则实数m的取值范围是 .