题目内容
已知 ,若存在区间
,若存在区间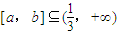 ,使得{y|y=f(x),x⊆[a,b]}=[ma,mb],则实数m的取值范围是 .
,使得{y|y=f(x),x⊆[a,b]}=[ma,mb],则实数m的取值范围是 .
【答案】分析:首先分析出函数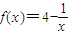 在区间[a,b]上为增函数,然后由题意得到
在区间[a,b]上为增函数,然后由题意得到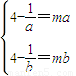 ,说明方程
,说明方程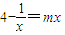 有两个大于
有两个大于 实数根,分离参数m,然后利用二次函数求m的取值范围.
实数根,分离参数m,然后利用二次函数求m的取值范围.
解答:解:因为函数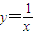 在
在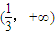 上为减函数,所以函数
上为减函数,所以函数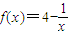 在
在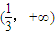 上为增函数,
上为增函数,
因为区间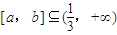 ,
,
由{y|y=f(x),x∈[a,b]}=[ma,mb],
则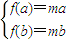 ,即
,即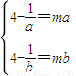 .
.
说明方程 有两个大于
有两个大于 实数根.
实数根.
由 得:
得: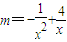 .
.
零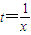 ,则t∈(0,3).
,则t∈(0,3).
则m=-t2+4t=-(t-2)2+4.
由t∈(0,3),所以m∈(0,4].
所以使得{y|y=f(x),x∈[a,b]}=[ma,mb]的实数m的取值范围是(0,4].
故答案为(0,4].
点评:本题考查了函数的定义域及其求法,考查了单调函数定义域及值域的关系,训练了二次函数值域的求法,考查了数学转化思想,是中档题.
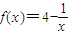 在区间[a,b]上为增函数,然后由题意得到
在区间[a,b]上为增函数,然后由题意得到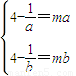 ,说明方程
,说明方程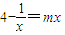 有两个大于
有两个大于 实数根,分离参数m,然后利用二次函数求m的取值范围.
实数根,分离参数m,然后利用二次函数求m的取值范围.解答:解:因为函数
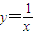 在
在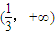 上为减函数,所以函数
上为减函数,所以函数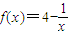 在
在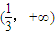 上为增函数,
上为增函数,因为区间
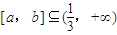 ,
,由{y|y=f(x),x∈[a,b]}=[ma,mb],
则
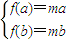 ,即
,即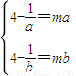 .
.说明方程
 有两个大于
有两个大于 实数根.
实数根.由
 得:
得: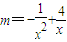 .
.零
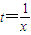 ,则t∈(0,3).
,则t∈(0,3).则m=-t2+4t=-(t-2)2+4.
由t∈(0,3),所以m∈(0,4].
所以使得{y|y=f(x),x∈[a,b]}=[ma,mb]的实数m的取值范围是(0,4].
故答案为(0,4].
点评:本题考查了函数的定义域及其求法,考查了单调函数定义域及值域的关系,训练了二次函数值域的求法,考查了数学转化思想,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
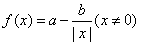 。
。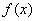 是
是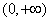 上的增函数,求实数
上的增函数,求实数 的取值范围;
的取值范围;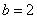 时,若不等式
时,若不等式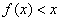 在区间
在区间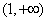 上恒成立,求实数
上恒成立,求实数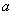 的取值范围;
的取值范围;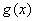 若存在区间
若存在区间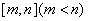 ,使
,使 时,函数
时,函数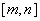 ,则称
,则称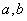 应满足的条件。
应满足的条件。