题目内容
对于任意非零实数x,y,函数y=f(x)(x≠0)满足f(xy)=f(x)+f(y).(1)求证:f(1)=f(-1)=0;
(2)求证:y=f(x)是偶函数;
(3)若y=f(x)在(0,+∞)上是增函数,解不等式f(x)+f(x-![]() )≤0.
)≤0.
(1)证明:令x=y=1,得f(1)=f(1)+f(1),则f(1)=0;又令x=y=-1,得f(1)=f(-1)+f(-1),即0=2f(-1),
∴f(-1)=0,故f(1)=f(-1)=0.
(2)证明:∵f(1)=f(x·![]() )=f(x)+f(
)=f(x)+f(![]() ),f(-1)=f(-x·
),f(-1)=f(-x·![]() )=f(-x)+f(
)=f(-x)+f(![]() ),而f(1)=f(-1)=0,
),而f(1)=f(-1)=0,
∴f(-x)=f(x),
∴f(x)是偶函数,
(3)解析:∵f(x)+f(x-![]() )≤0,即f(x2-
)≤0,即f(x2-![]() x)≤0,而y=f(x)在(0,+∞)上是增函数,
x)≤0,而y=f(x)在(0,+∞)上是增函数,
∴f(x2-![]() x)≤f(1),
x)≤f(1),
∴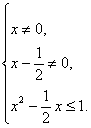
解得 ![]() ≤x≤
≤x≤![]() ,且x≠0,x≠
,且x≠0,x≠![]() .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目