题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(1)试判断直线![]() :
:![]() 与圆的位置关系;
与圆的位置关系;
(2)设弦![]() 的中点为
的中点为![]() ,求
,求![]() 的轨迹方程.
的轨迹方程.
【答案】(1)直线与圆相交;(2)![]() .
.
【解析】
(1)由直线![]() :
:![]() 可知过定点
可知过定点![]() ,求圆心
,求圆心![]()
![]() 到
到![]() 的距离
的距离![]() ,与半径2比较,通过判断点
,与半径2比较,通过判断点![]() 和圆的位置关系,即可得出直线
和圆的位置关系,即可得出直线![]() 与圆的位置关系;
与圆的位置关系;
(2)分类讨论,当点![]() 与点
与点![]() 不重合时,利用圆的性质得出
不重合时,利用圆的性质得出![]() ,运用向量垂直的坐标运算,即可得出
,运用向量垂直的坐标运算,即可得出![]() 的轨迹方程;当点
的轨迹方程;当点![]() 与点
与点![]() 重合,即
重合,即![]() ,
,![]() 时,也满足上式;综合得出轨迹方程.
时,也满足上式;综合得出轨迹方程.
(1)由圆的方程可知,圆心![]()
![]() ,半径为2,
,半径为2,
因为直线![]() 过定点
过定点![]() ,且
,且![]() ,
,
所以![]() 点在圆内,故直线
点在圆内,故直线![]() :
:![]() 与圆相交.
与圆相交.
(2)由圆的性质知:当点![]() 与点
与点![]() 不重合时,
不重合时,
则![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
则![]() .
.
当点![]() 与点
与点![]() 重合,即
重合,即![]() ,
,![]() 时,也满足上式.
时,也满足上式.
∴点![]() 的轨迹方程为
的轨迹方程为![]() .
.

练习册系列答案
相关题目
【题目】某家庭为了解冬季用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出用电量![]() 关于气温
关于气温![]() 的线性回归方程;
的线性回归方程;
(2)在这5天中随机抽取两天,求至少有一天用电量低于10(度)的概率.
(附:回归直线方程的斜率和截距的最小二乘法估计公式为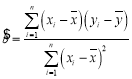 ,
,![]() )
)

