题目内容
设 .
.(1)设an=f(n)-g(n),求a1,a2,a3,并证明{an}为递减数列;
(2)是否存在常数c,使f(n)-g(n)>c对n∈N*恒成立?若存在,试找出c的一个值,并证明;若不存在,说明理由.
【答案】分析:(1)由“ ”,可得到a1,a2,a3,再由通项公式求得an+1-an,再判断它与0的大小,从而判断是否为递减的等差数列.
”,可得到a1,a2,a3,再由通项公式求得an+1-an,再判断它与0的大小,从而判断是否为递减的等差数列.
(2)对于存在性问题,可先假设存在,即假设存在常数c,使f(n)-g(n)>c对n∈N*恒成立,再利用ln(1+x)<x对x>0恒成立,通过取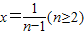 即可得到证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.
即可得到证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)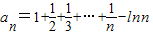 .
.
由此a1=1.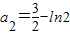 ,
,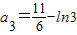 .
.
又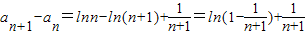 .
.
构造函数h(x)=ln(1-x)+x.x∈(0,1)
由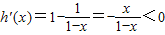
知h(x)在[0,1)上为单减函数.
从而当x>0时,h(x)<h(0)=0
取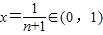 .有
.有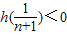
即an+1-an<0
故{an}为递减数列.
(2)存在如C=0等,下证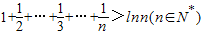
注意到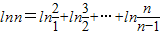 .
.
这只要证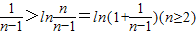 即可.
即可.
∵ln(1+x)<x对x>0恒成立,
∴取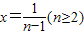 即可得上式成立.
即可得上式成立.
从而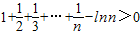
此时常数c=0.
点评:本题主要考查函数与数列的综合运用,主要涉及了数列的定义,通项,不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
 ”,可得到a1,a2,a3,再由通项公式求得an+1-an,再判断它与0的大小,从而判断是否为递减的等差数列.
”,可得到a1,a2,a3,再由通项公式求得an+1-an,再判断它与0的大小,从而判断是否为递减的等差数列.(2)对于存在性问题,可先假设存在,即假设存在常数c,使f(n)-g(n)>c对n∈N*恒成立,再利用ln(1+x)<x对x>0恒成立,通过取
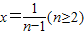 即可得到证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.
即可得到证明,若出现矛盾,则说明假设不成立,即不存在;否则存在.解答:解:(1)
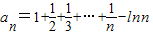 .
.由此a1=1.
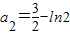 ,
,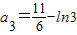 .
.又
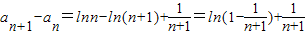 .
.构造函数h(x)=ln(1-x)+x.x∈(0,1)
由
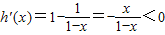
知h(x)在[0,1)上为单减函数.
从而当x>0时,h(x)<h(0)=0
取
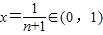 .有
.有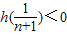
即an+1-an<0
故{an}为递减数列.
(2)存在如C=0等,下证
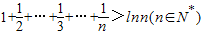
注意到
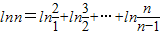 .
.这只要证
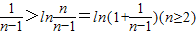 即可.
即可.∵ln(1+x)<x对x>0恒成立,
∴取
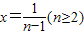 即可得上式成立.
即可得上式成立.从而
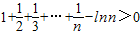
此时常数c=0.
点评:本题主要考查函数与数列的综合运用,主要涉及了数列的定义,通项,不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数f(x)=-
,设an=
,若-1≤x1<0<x2<x3,则( )
| x+1 |
| f(xn)-2 |
| xn |
| A、a2<a3<a1 |
| B、a1<a2<a3 |
| C、a1<a3<a2 |
| D、a3<a2<a1 |
 .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.