题目内容
设函数f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在(1,f(1))点处的切线的方程;
(2)求函数f(x)的单调区间与极值;
(3)已知函数g(x)=f(x)+![]() 有三个互不相同的零点,求m的取值范围.
有三个互不相同的零点,求m的取值范围.
解析 (1)当m=1时,f(x)=-![]() x3+x2,f′(x)=-x2+2x,故f′(1)=1.
x3+x2,f′(x)=-x2+2x,故f′(1)=1.
所以曲线y=f(x)在点(1,f(1))处的切线斜率为1.
切线方程为3x-3y-1=0.
(2)f′(x)=-x2+2x+m2-1,令f′(x)=0,得到x=1-m或x=1+m.
因为m>0,所以1+m>1-m.
当x变化时,f(x),![]() f′(x)的变化情况如下表:
f′(x)的变化情况如下表:
| x | (-∞,1-m) | 1-m | (1-m,1+m) | 1+m | (1+m,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) |
| 极小值 |
| 极大值 |
|
f′(x)在(-∞,1-m)和(1+m,+∞)内减函数,在(1-m,1+m)内增函数.
函数f(x)在x=1+m处取得极大值f(1+m),且f(1+m)=![]() m3+m2-
m3+m2-![]() .
.
函数f(x)在x=1-m处取得极小值f(1-m),
且f(1-m)=-![]() m3+m2-
m3+m2-![]() .
.
(3)由(2)知,
函数g(x)在x=1+m处取得极大值g(1+m)=f(1+m)+![]() ,
,
且g(1+m)=![]() m3+m2.
m3+m2.
函数g(x)在x=1-m处取得极小值g(1-m)=f(1-m)+![]() ,
,
且g(1-m)=-![]() m3+m2.
m3+m2.
根据三次函数的图像与性质,函数g(x)=f(x)+![]() 有三个互不相同的零点,只需要
有三个互不相同的零点,只需要
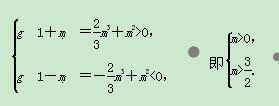 所以m的取值范围是
所以m的取值范围是![]() .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目