题目内容
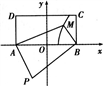
2008年5月12日，四川汶川发生里氏8.0级地震，为了援救灾民，某部队在如图所示的P处空降了一批救灾药品，今要把这批药品沿道路PA、PB送到矩形灾民区AB-CD中去，已知PA=100 km．PB=150 km．BC=60 km，∠APB=60°，试在灾民区中确定一条界线，使位于界线一侧的点沿道路PA送药较近，而另一侧的点沿道路PB送药较近，请说明这一界线是一条什么曲线？并求出其方程．
解：矩形灾民区ABCD 中的点可分为三类，
第一类沿道路PA 送药较近，
第二类沿道路PB 送药较近，
第三类沿道路PA 和PB 送药一样远近．
依题意，界线是第三类点的轨迹．
设M为界线上的任一点，则|PA|+|MA|=|PB|+|MB|，|MA|-|MB|=|PB|-|PA|=50（定值）．
∴界线是以A、B为焦点的双曲线的右支的一部分．
如图，以AB所在直线为x轴，线段AB的垂直平分线为y轴，建立平面直角坐标系，
设所求双曲线方程的标准形式为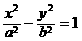
(a>0，b>0)，
∵ a= 25,2c=|AB|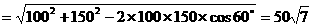
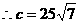,b2 =c2-a2=3750,
故双曲线的标准方程为
注意到点C的坐标为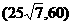
，故y的最大值为60，
此时x=35，故界线的曲线方程为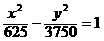
(25≤x≤35,y>0)．
第一类沿道路PA 送药较近，
第二类沿道路PB 送药较近，
第三类沿道路PA 和PB 送药一样远近．
依题意，界线是第三类点的轨迹．
设M为界线上的任一点，则|PA|+|MA|=|PB|+|MB|，|MA|-|MB|=|PB|-|PA|=50（定值）．
∴界线是以A、B为焦点的双曲线的右支的一部分．
如图，以AB所在直线为x轴，线段AB的垂直平分线为y轴，建立平面直角坐标系，
设所求双曲线方程的标准形式为
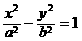(a>0，b>0)，∵ a= 25,2c=|AB|
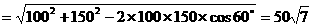
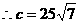,b2 =c2-a2=3750,故双曲线的标准方程为
注意到点C的坐标为
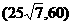，故y的最大值为60，此时x=35，故界线的曲线方程为
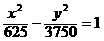(25≤x≤35,y>0)．
练习册系列答案
相关题目
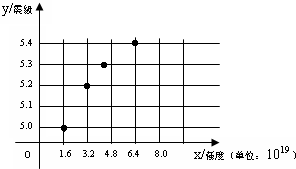2008年5月12日，四川汶川地区发生里氏8.0级特大地震．在随后的几天中，地震专家对汶川地区发生的余震进行了监测，记录的部分数据如下表：| 强度（J） | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
| 震级（里氏） | 5.0 | 5.2 | 5.3 | 5.4 |
地震强度（x）和震级（y）的模拟函数关系可以选用y=algx+b（其中a，b为常数）．利用散点图可知 a的值等于