题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,已知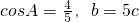 .
.
(1)求sinC的值;
(2)若a=6,求△ABC的面积S的值.
解:(1)∵cosA= ,b=5c,
,b=5c,
∴a2=b2+c2-2bccosA=25c2+c2-10c2× =18c2,
=18c2,
∴a=3 c,
c,
∵cosA= ,0<A<π,
,0<A<π,
∴sinA=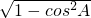 =
= ,
,
∵ =
= ,
,
∴sinC=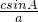 =
=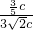 =
= ;
;
(2)由(1)a=3 c,a=6,
c,a=6,
∴c= ,
,
∵b=5c,
∴b=5 ,又sinA=
,又sinA= ,
,
∴S= bcsinA=
bcsinA= ×5
×5 ×
× ×
× =3.
=3.
分析:(1)利用余弦定理得到a2=b2+c2-2bccosA,将cosA及b=5c代入,整理后用c表示出a,再由cosA的值及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,再由表示出的a及c,利用正弦定理即可求出sinC的值;
(2)由a的值及用c表示出的a,求出c的值,进而再由b=5c求出b的值,最后由b,c及sinA的值,利用三角形的面积公式即可求出三角形ABC的面积S.
点评:此题考查了正弦、余弦定理,三角形的面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.
 ,b=5c,
,b=5c,∴a2=b2+c2-2bccosA=25c2+c2-10c2×
 =18c2,
=18c2,∴a=3
 c,
c,∵cosA=
 ,0<A<π,
,0<A<π,∴sinA=
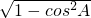 =
= ,
,∵
 =
= ,
,∴sinC=
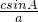 =
=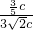 =
= ;
;(2)由(1)a=3
 c,a=6,
c,a=6,∴c=
 ,
,∵b=5c,
∴b=5
 ,又sinA=
,又sinA= ,
,∴S=
 bcsinA=
bcsinA= ×5
×5 ×
× ×
× =3.
=3.分析:(1)利用余弦定理得到a2=b2+c2-2bccosA,将cosA及b=5c代入,整理后用c表示出a,再由cosA的值及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,再由表示出的a及c,利用正弦定理即可求出sinC的值;
(2)由a的值及用c表示出的a,求出c的值,进而再由b=5c求出b的值,最后由b,c及sinA的值,利用三角形的面积公式即可求出三角形ABC的面积S.
点评:此题考查了正弦、余弦定理,三角形的面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |