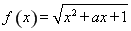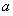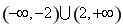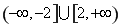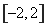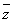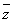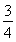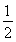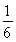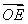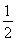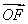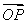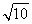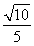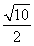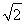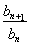题目内容
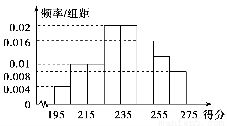
某高校组织自主招生考试，共有2 000名优秀同学参加笔试，成绩均介于195分到275分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成8组：第1组[195,205)，第2组[205,215)，…，第8组[265,275]．如图是按上述分组方法得到的频率分布直方图，且笔试成绩在260分(含260分)以上的同学进入面试．
(1)估计所有参加笔试的2 000名同学中，参加面试的同学人数；
(2)面试时，每位同学抽取两个问题，若两个问题全答错，则不能取得该校的自主招生资格；若两个问题均回答正确且笔试成绩在270分以上，则获A类资格；其他情况下获B类资格．现已知某中学有两人获得面试资格，且仅有一人笔试成绩为270分以上，在回答两个面试问题时，两人对每一个问题正确回答的概率均为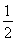
，求恰有一名同学获得该高校B类资格的概率．
（1）280人（2）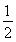
【解析】(1)设第i(i＝1,2，…，8)组的频率为fi，则由频率分布直方图知f7＝1－(0.004＋0.01＋0.01＋0.02＋0.02＋0.016＋0.008)×10＝0.12.
所以成绩在260分以上的同学的概率P≈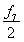
＋f8＝0.14，
∴2 000×0.14＝280，
故这2 000名同学中，取得面试资格的约为280人．
(2)不妨设两名同学分别为M，N，且M的笔试成绩在270分以上，则对于M，答题的可能有M11，M10，M01，M00，对于N，答题的可能有N11，N10，N01，N00，其中角标中的1表示正确，0表示错误，如N10表示N同学第一题正确，第二题错误．
将两名同学的答题情况列表如下：
| M11 | M10 | M01 | M00 |
N11 | AB | BB | BB | CB |
N10 | AB | BB | BB | CB |
N01 | AB | BB | BB | CB |
N00 | AC | BC | BC | CC |
表中AB表示M获A类资格，N获B类资格；BC表示M获B类资格，N没有获得资格．
所以恰有一名同学获得该高校B类资格的概率为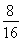
＝.
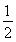