题目内容
（本小题满分12分）
如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC,PA=AB=BC=2
（1）求证：平面AEF⊥平面PBC；
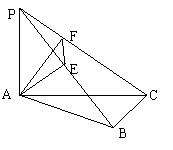（2）求二面角P—BC—A的大小。
（本小题满分12分）
如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC,PA=AB=BC=2
（1）求证：平面AEF⊥平面PBC；
（2）求二面角P—BC—A的大小。
(1)证：∵PA⊥平面ABC，
∴ PA⊥BC
又AB⊥BC，AB与PA相交于点A，∴BC⊥平面PAB，
∴BC⊥AE，又AE⊥PB，而PB与BC相交于点B，∴AE⊥平面PBC
故，平面AEF⊥平面PBC………… 6分
（2）由(1)知，BC⊥平面PAB，
∴PB⊥BC
又AB⊥BC，∴∠PBA就是二面角P—BC—A的平面角，
在RｔΔPAB中，∵PA=AB，∴∠PBA=450，即二面角P—BC—A的大小为450。… 12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
