题目内容
设点M、N分别是不等边△ABC的重心与外心,已知A(0,1),B(0,-1),且 .
.(1)求动点C的轨迹E;
(2)若直线y=x+b与曲线E交于不同的两点P、Q,且满足
 ,求实数b的取值.
,求实数b的取值.
【答案】分析:(1)设点C(x,y ),则点M (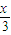 ,
,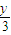 ),由
),由 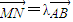 ,可得 MN∥AB,故N的横坐标等于
,可得 MN∥AB,故N的横坐标等于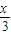 ,又N在AB的中垂线上,故纵坐标等于 0.由于 NA=NC,可得
,又N在AB的中垂线上,故纵坐标等于 0.由于 NA=NC,可得 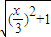 =
=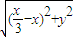 ,化简可得轨迹方程,从而得到轨迹.
,化简可得轨迹方程,从而得到轨迹.
(2)把直线y=x+b代入轨迹E的方程化简可得 4x2+6bx+3b2-3=0,由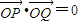 可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0,把根与系数的关系代入求出b值.
可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0,把根与系数的关系代入求出b值.
解答:解:(1)设点C(x,y ),则 点M (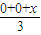 ,
,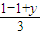 ),即 点M (
),即 点M (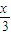 ,
,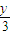 ),
),
由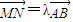 ,可得 MN∥AB,故N的横坐标等于
,可得 MN∥AB,故N的横坐标等于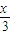 ,又N在AB的中垂线上,故纵坐标等于 0.
,又N在AB的中垂线上,故纵坐标等于 0.
由于N是不等边△ABC的外心,∴NA=NC,∴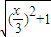 =
=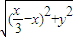 .
.
化简可得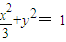 ,xy≠0,故动点C的轨迹E是焦点在x轴上的标准位置的一个椭圆,去掉其顶点.
,xy≠0,故动点C的轨迹E是焦点在x轴上的标准位置的一个椭圆,去掉其顶点.
(2)把直线y=x+b代入轨迹E的方程化简可得 4x2+6bx+3b2-3=0.由题意可得,b≠0,b≠±1,
且△=36b2-16( 3b2-3)>0,x1+x2=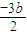 ,x1•x2=
,x1•x2=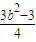 .
.
由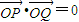 可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0.
可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0.
∴2•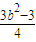 +b•(
+b•( 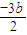 )+b2=0,解得 b2=
)+b2=0,解得 b2= ,∴b=±
,∴b=±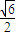 .
.
点评:本题考查点轨迹方程的求法,直线和圆锥曲线的位置关系,判断轨迹E的形状,是阶梯的易错点.
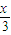 ,
,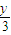 ),由
),由 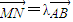 ,可得 MN∥AB,故N的横坐标等于
,可得 MN∥AB,故N的横坐标等于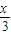 ,又N在AB的中垂线上,故纵坐标等于 0.由于 NA=NC,可得
,又N在AB的中垂线上,故纵坐标等于 0.由于 NA=NC,可得 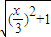 =
=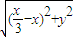 ,化简可得轨迹方程,从而得到轨迹.
,化简可得轨迹方程,从而得到轨迹.(2)把直线y=x+b代入轨迹E的方程化简可得 4x2+6bx+3b2-3=0,由
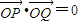 可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0,把根与系数的关系代入求出b值.
可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0,把根与系数的关系代入求出b值.解答:解:(1)设点C(x,y ),则 点M (
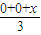 ,
,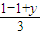 ),即 点M (
),即 点M (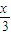 ,
,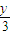 ),
),由
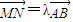 ,可得 MN∥AB,故N的横坐标等于
,可得 MN∥AB,故N的横坐标等于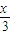 ,又N在AB的中垂线上,故纵坐标等于 0.
,又N在AB的中垂线上,故纵坐标等于 0.由于N是不等边△ABC的外心,∴NA=NC,∴
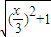 =
=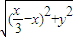 .
.化简可得
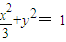 ,xy≠0,故动点C的轨迹E是焦点在x轴上的标准位置的一个椭圆,去掉其顶点.
,xy≠0,故动点C的轨迹E是焦点在x轴上的标准位置的一个椭圆,去掉其顶点.(2)把直线y=x+b代入轨迹E的方程化简可得 4x2+6bx+3b2-3=0.由题意可得,b≠0,b≠±1,
且△=36b2-16( 3b2-3)>0,x1+x2=
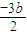 ,x1•x2=
,x1•x2=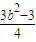 .
.由
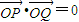 可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0.
可得 x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0.∴2•
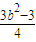 +b•(
+b•( 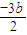 )+b2=0,解得 b2=
)+b2=0,解得 b2= ,∴b=±
,∴b=±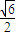 .
.点评:本题考查点轨迹方程的求法,直线和圆锥曲线的位置关系,判断轨迹E的形状,是阶梯的易错点.

练习册系列答案
相关题目
 .
. ,求实数b的取值范围.
,求实数b的取值范围. 、
、 ,且
,且 .
. 与曲线E交于不同的两点P、Q,且满足
与曲线E交于不同的两点P、Q,且满足 ,求实数
,求实数 的取值范围。
的取值范围。 、
、 ,且
,且 .
. 与曲线E交于不同的两点P、Q,且满足
与曲线E交于不同的两点P、Q,且满足 ,求实数
,求实数 的取值范围。
的取值范围。