题目内容
求证:三个平面两两互相垂直,其中两个平面的交线必与第三个平面垂直.
答案:略
解析:
提示:
解析:
|
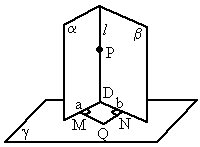
如图,已知:a ⊥b ,b ⊥g ,g ⊥a ,a ∩b =l.求证:l⊥g .证明:在 l上取一点P,且
(2) 另一证法:在g 内任取一点Q,过 Q作QM⊥a于M,作ON⊥b于N.∵a ⊥g ,b ⊥g ,∴ QM⊥a ,QN⊥b ,∴QM⊥l,QN⊥l,∴l⊥g . |
提示:
|
这一问题可以找出很多具体的模型,如正方体的过同一顶点的三个面,再如墙角处的三面墙等,我们应先将其数学化再解决. (1)本题的条件过强,可以减弱为a ⊥b ,b ⊥g ,a ∩b =l,求证:l⊥g ,即a ⊥b 用不到,但本题考虑到这是现实中常见的模型,所以这样出题. |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目

 两两所成的角相等,且
两两所成的角相等,且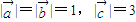 ,则
,则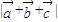 = .
= .