题目内容
(8分)设(3x-1)8=a8x8+a7x7+…+a1x+a0.求:
(1)a8+a7+…+a1;
(2)a8+a6+a4+a2+a0.
(1)a8+a7+…+a1;
(2)a8+a6+a4+a2+a0.
32 896.
对于二项式展开式的系数求和问题,通常采用赋值法求解,一般赋给字母的值为0,-1,1等。
解:令x=0,得a0=1.
(1)令x=1得(3-1)8=a8+a7+…+a1+a0,①
∴a8+a7+…+a2+a1=28-a0=256-1=255.
(2)令x=-1得(-3-1)8=a8-a7+a6-…-a1+a0.②
①+②得28+48=2(a8+a6+a4+a2+a0),
∴a8+a6+a4+a2+a0= (28+48)=32 896.
(28+48)=32 896.
解:令x=0,得a0=1.
(1)令x=1得(3-1)8=a8+a7+…+a1+a0,①
∴a8+a7+…+a2+a1=28-a0=256-1=255.
(2)令x=-1得(-3-1)8=a8-a7+a6-…-a1+a0.②
①+②得28+48=2(a8+a6+a4+a2+a0),
∴a8+a6+a4+a2+a0=
 (28+48)=32 896.
(28+48)=32 896.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,则
,则 的值为
的值为



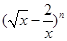 的展开式中,第4项和第9项的二项式系数相等,
的展开式中,第4项和第9项的二项式系数相等,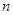 ,
,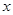 的一次项的系数.
的一次项的系数.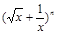 的展开式中各项系数和为64.
的展开式中各项系数和为64.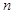 ;
;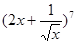 的二项展开式中
的二项展开式中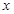 的系数是____ (用数学作答).
的系数是____ (用数学作答). 展开式中
展开式中 的系数为10, 则实数
的系数为10, 则实数 的值为
的值为  ,
,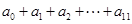 的值为( )
的值为( )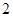



 的展开式中,
的展开式中, 的系数是( )
的系数是( )

