题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() , 若椭圆上一点
, 若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 是点
是点![]() 在
在![]() 轴上的垂足,延长
轴上的垂足,延长![]() 交椭圆
交椭圆![]() 于
于![]() ,求证:
,求证: ![]() 三点共线.
三点共线.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由椭圆定义可得![]() ,再通过点在椭圆上求得
,再通过点在椭圆上求得![]() ,进而得椭圆方程;
,进而得椭圆方程;
(2)由题知直线![]() 的斜率必存在,设
的斜率必存在,设![]() 的方程为
的方程为![]() ,点
,点![]() ,直线与椭圆联立得
,直线与椭圆联立得![]() ,由题可得直线
,由题可得直线![]() 方程为
方程为![]() ,由
,由![]() 化简直线
化简直线![]() 方程为
方程为![]() ,令
,令![]() ,可得直线
,可得直线![]() 过点
过点![]() ,进而得证.
,进而得证.
试题解析:
(1)依题意, ![]() ,故
,故![]() ,将
,将![]() 代入
代入![]() 中,
中,
解得![]() ,故椭圆
,故椭圆![]() ;
;
(2)由题知直线![]() 的斜率必存在,设
的斜率必存在,设![]() 的方程为
的方程为![]() ,
,
点![]() ,联立
,联立![]() 得
得![]() ,
,
即![]() ,
,
由题可得直线![]() 方程为
方程为![]() ,
,
又∵![]() ,
,
∴直线![]() 方程为
方程为![]() ,
,
令![]() ,整理得
,整理得![]()
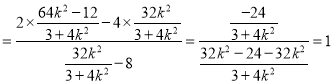 ,即直线
,即直线![]() 过点
过点![]() ,
,
又∵椭圆![]() 的右焦点坐标为
的右焦点坐标为![]() , ∴三点
, ∴三点![]() 在同一条直线上.
在同一条直线上.

练习册系列答案
相关题目
【题目】已知点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 的右顶点,点
的右顶点,点![]() 是椭圆
是椭圆![]() 上不同的两点(均异于
上不同的两点(均异于![]() )且满足直线
)且满足直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .试判断直线
.试判断直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由.
是否过定点,若是,求出定点坐标,若不是,说明理由.
【题目】某化工厂为预测产品的回收率![]() ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量![]() 之间的相关关系,现收集了4组对照数据。
之间的相关关系,现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据相关系数![]() 的大小判断回收率
的大小判断回收率![]() 与
与![]() 之间是否存在高度线性相关关系;
之间是否存在高度线性相关关系;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测当
,并预测当![]() 时回收率
时回收率![]() 的值.
的值.
参考数据: 
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
 ,
, ![]()
