题目内容
下列命题:
①命题“事件A与B互斥”是“事件A与B对立”的必要不充分条件;
②“am2<bm2”是“a<b”的充分必要条件;
③“矩形的两条对角线相等”的否命题为假;
④在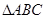 中,“
中,“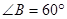 ”是
”是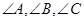 三个角成等差数列的充要条件;
三个角成等差数列的充要条件;
⑤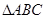 中,若
中,若 ,则
,则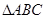 为直角三角形.
为直角三角形.
判断错误的有___________.
②⑤
【解析】
试题分析:事件A与B互斥,事件A与B不一定对立;反之事件A与B对立,一定有事件A与B互斥.所以“事件A与B互斥”是“事件A与B对立”的必要不充分条件.所以命题①正确.由am2<bm2知m2>0,不等式两边同乘以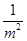 得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,故am2<bm2是a<b的充分不必要条件,故命题②不正确.原命题:矩形的两条对角线相等.则其否命题为:若四边形不是矩形,则其对角线不相等.此否命题为假命题,如等腰梯形不是矩形,但其对角线相等,故命题③正确.在△ABC中,若∠B=60°,因为∠A+∠B+∠C=180°,得∠A+∠C=180°-∠B=180°-60°=120°,所以2∠B=∠A+∠C,所以∠A,∠B,∠C三个角成等差数列.若∠A,∠B,∠C三个角成等差数列,可设公差为d,则∠A=∠B-d,∠C=∠B+d,由∠A+∠B+∠C=180°,得∠B-d+∠B+∠b+d=180°,∴∠B=60°.所以在△ABC中,“∠B=60°”是∠A,∠B,∠C三个角成等差数列的充要条件,故命题④正确.在△ABC中,若sinA=cosB,则sinA=sin(90°-B),所以A=90°-B或A+90°-B=180°,所以A+B=90°或A-B=90°,则△ABC不一定为直角三角形,故命题⑤不正确.故答案为②⑤.
得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,故am2<bm2是a<b的充分不必要条件,故命题②不正确.原命题:矩形的两条对角线相等.则其否命题为:若四边形不是矩形,则其对角线不相等.此否命题为假命题,如等腰梯形不是矩形,但其对角线相等,故命题③正确.在△ABC中,若∠B=60°,因为∠A+∠B+∠C=180°,得∠A+∠C=180°-∠B=180°-60°=120°,所以2∠B=∠A+∠C,所以∠A,∠B,∠C三个角成等差数列.若∠A,∠B,∠C三个角成等差数列,可设公差为d,则∠A=∠B-d,∠C=∠B+d,由∠A+∠B+∠C=180°,得∠B-d+∠B+∠b+d=180°,∴∠B=60°.所以在△ABC中,“∠B=60°”是∠A,∠B,∠C三个角成等差数列的充要条件,故命题④正确.在△ABC中,若sinA=cosB,则sinA=sin(90°-B),所以A=90°-B或A+90°-B=180°,所以A+B=90°或A-B=90°,则△ABC不一定为直角三角形,故命题⑤不正确.故答案为②⑤.
考点:本题考查了判断命题的真假及充要条件判断.
点评:最常用的方法是定义法,即“若p?q,则p是q的充分条件”;“若q?p,则p是q成立的必要条件”;“若p?q,则p是q的充要条件”

 阅读快车系列答案
阅读快车系列答案