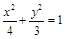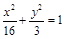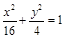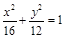题目内容
过点 且与抛物线
且与抛物线 只有一个公共点的直线有( ).
只有一个公共点的直线有( ).
A. 条 条 | B. 条 条 | C.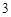 条 条 | D. 条 条 |
C
解析试题分析:过点 斜率不存在的直线为
斜率不存在的直线为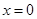 满足与
满足与 只有一个公共点,当斜率存在时,设直线为
只有一个公共点,当斜率存在时,设直线为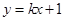 ,与
,与 联立整理得
联立整理得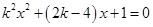 ,当
,当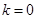 时,方程是一次方程,有一个解,满足一个交点,当
时,方程是一次方程,有一个解,满足一个交点,当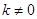 时由
时由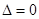 可得
可得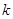 值有一个,即有一个公共点,所以满足题意的直线有3条
值有一个,即有一个公共点,所以满足题意的直线有3条
考点:直线与抛物线的位置关系
点评:要满足直线与抛物线有一个公共点只需联立方程后有唯一解,此时注意设直线方程要分斜率存在与不存在两种情况

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知双曲线 的两条渐近线均与
的两条渐近线均与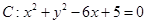 相切,则该双曲线离心率等于
相切,则该双曲线离心率等于
A.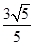 | B.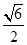 | C.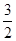 | D.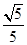 |
将两个顶点在抛物线 上,另一个顶点
上,另一个顶点 ,这样的正三角形有( )
,这样的正三角形有( )
| A.0个 | B.2个 | C.4个 | D.1个 |
如图,F1,F2是双曲线C: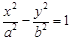 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与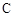 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
A.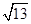 | B.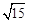 |
| C.2 | D.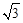 |
若点O和点F分别为椭圆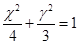 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则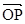 ·
·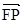 的最大值为( ).
的最大值为( ).
| A.2 | B.3 | C.6 | D.8 |
已知抛物线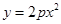 (p>0)的准线与圆
(p>0)的准线与圆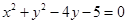 相切,则p的值为( )
相切,则p的值为( )
| A.10 | B.6 | C.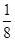 | D.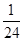 |
 的离心率为
的离心率为 ,双曲线
,双曲线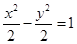 的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )
的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )
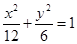


 ,
,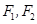 为其两个焦点,点
为其两个焦点,点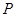 为双曲线上一点,若
为双曲线上一点,若 ,则
,则 的值为________.
的值为________.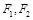 为椭圆
为椭圆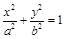 (
(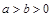 )的两个焦点,过F2作椭圆的弦AB,若
)的两个焦点,过F2作椭圆的弦AB,若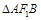 的周长为16,椭圆的离心率
的周长为16,椭圆的离心率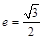 ,则椭圆的方程为( )
,则椭圆的方程为( )