Question

平行四边形的一个顶点A在平面a内，其余顶点在a的同侧，已知其中有两个顶点到a的距离分别为1和2，那么剩下的一个顶点到平面a的距离可能是：
①1；②2； ③3；④4；
以上结论正确的为

 

．（写出所有正确结论的编号）

Answer 1

分析：由已知中平行四边形的一个顶点A在平面a内，其余顶点在a的同侧，根据平行四边形对角线上两顶点到平面α的距离的和相等，我们可以根据A到α距离为0，另外三个顶点中有两个顶点到a的距离分别为1和2，分类讨论，即可得到答案．

解答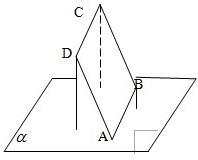：解：如图，B、D到平面a的距离为1、2，则D、B的中
点到平面a的距离为

3

2

，所以C到平面a的距离为3；
B、C到平面a的距离为1、2，D到平面a的距离为x，
则x+1=2或x+2=1，即x=1，所以D到平面a的距
离为1；
C、D到平面a的距离为1、2，同理可得B到平面a的距
离为1；所以选①③．
故答案为：①③

点评：本题考查的知识点是空间中点、线、面之间的距离，其中根据行四边形对角线上两顶点到平面α的距离的和相等，结论其它条件进行分类讨论，是解答本题的关键．