题目内容
6.已知四面体OABC各棱长为1,D是棱OA的中点,则异面直线BD与AC所成角的余弦值是$\frac{\sqrt{3}}{6}$.分析 先画出四面体OABC,取棱OC中点E,连接DE,BE,可判断∠BDE便是异面直线BD与AC所成角,并容易求出$BD=BE=\frac{\sqrt{3}}{2},DE=\frac{1}{2}$,这样便可得到cos∠BDE=$\frac{\frac{1}{2}DE}{BD}$.
解答 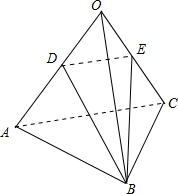 解:如图,取OC中点E,连接DE,BE;
解:如图,取OC中点E,连接DE,BE;
∵D是棱OA的中点;
∴DE∥AC;
∴∠BDE或其补角为直线BD,AC所成角;
则在△BDE中,BD=BE=$\frac{\sqrt{3}}{2}$,DE=$\frac{1}{2}$;
∴$cos∠BDE=\frac{\frac{1}{4}}{\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{6}$;
∴∠BDE为异面直线BD,AC所成角,其余弦值为$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 三角形中位线的性质,异面直线所成角的概念及求法,以及直角三角形边角的关系.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
1.在复平面内,与复数z=-3+4i的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
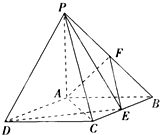 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动. 对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85,正确的是( )
对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85,正确的是( )