题目内容
记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,y0)为坐标的点是函数f(x)的图象上的“稳定点”.
(1)若函数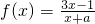 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
(2)已知定义在实数集R上的奇函数f(x)存在有限个“稳定点”,求证:f(x)必有奇数个“稳定点”.
解:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数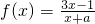 的图象上的两个“稳定点”,
的图象上的两个“稳定点”,
则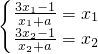 ,即有
,即有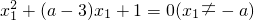 ,
,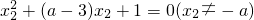 ,
,
∴x1,x2是方程x2+(a-3)x+1=0(x≠-a)的两根,
∴方程x2+(a-3)x+1=0有两个相异的实根且不等于-a,
∴ ,解得a>5或a<1且a
,解得a>5或a<1且a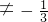 ,
,
∴a的取值范围是(-∞,- )∪(-
)∪(- ,1)∪(5,+∞;
,1)∪(5,+∞;
(2)∵f(x)是R上的奇函数,
∴f(0)=0,∴原点(0,0)是函数f(x)的“稳定点”,
若f(x)还有“稳定点”(x0,y0),
则由f(x)为奇函数,得f(-x0)=-f(x0)且f(x0)=x0,
∴f(-x0)=-x0,
这说明:(-x0,-x0)也是f(x)的“稳定点”.
综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点也是其“稳定点”,
所以它的“稳定点”的个数为奇数.
分析:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数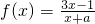 的图象上的两个“稳定点”,由定义可得
的图象上的两个“稳定点”,由定义可得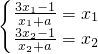 ,所以x1,x2是方程x2+(a-3)x+1=0(x≠-a)的两相异实根且不等于-a,由此可得关于a的不等式组,解出即可;
,所以x1,x2是方程x2+(a-3)x+1=0(x≠-a)的两相异实根且不等于-a,由此可得关于a的不等式组,解出即可;
(2)由f(x)为R上的奇函数可判断原点(0,0)是函数f(x)的“稳定点”,只要再说明除原点外“稳定点”成对出现即可;
点评:本题以新定义为切入点,主要考查了二次方程的根的个数问题、奇函数性质等知识的综合应用,考查学生分析解决新问题的能力.
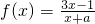 的图象上的两个“稳定点”,
的图象上的两个“稳定点”,则
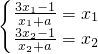 ,即有
,即有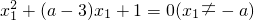 ,
,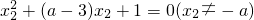 ,
,∴x1,x2是方程x2+(a-3)x+1=0(x≠-a)的两根,
∴方程x2+(a-3)x+1=0有两个相异的实根且不等于-a,
∴
 ,解得a>5或a<1且a
,解得a>5或a<1且a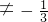 ,
,∴a的取值范围是(-∞,-
 )∪(-
)∪(- ,1)∪(5,+∞;
,1)∪(5,+∞;(2)∵f(x)是R上的奇函数,
∴f(0)=0,∴原点(0,0)是函数f(x)的“稳定点”,
若f(x)还有“稳定点”(x0,y0),
则由f(x)为奇函数,得f(-x0)=-f(x0)且f(x0)=x0,
∴f(-x0)=-x0,
这说明:(-x0,-x0)也是f(x)的“稳定点”.
综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点也是其“稳定点”,
所以它的“稳定点”的个数为奇数.
分析:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数
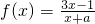 的图象上的两个“稳定点”,由定义可得
的图象上的两个“稳定点”,由定义可得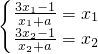 ,所以x1,x2是方程x2+(a-3)x+1=0(x≠-a)的两相异实根且不等于-a,由此可得关于a的不等式组,解出即可;
,所以x1,x2是方程x2+(a-3)x+1=0(x≠-a)的两相异实根且不等于-a,由此可得关于a的不等式组,解出即可;(2)由f(x)为R上的奇函数可判断原点(0,0)是函数f(x)的“稳定点”,只要再说明除原点外“稳定点”成对出现即可;
点评:本题以新定义为切入点,主要考查了二次方程的根的个数问题、奇函数性质等知识的综合应用,考查学生分析解决新问题的能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
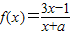 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;