题目内容
求曲线y=sinx与直线 ,
,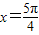 ,y=0所围成的平面图形的面积.
,y=0所围成的平面图形的面积.
【答案】分析:求曲线y=sinx与直线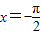 ,
, ,y=0所围成的平面图形的面积
,y=0所围成的平面图形的面积
解答:解:s= |sinx|dx=-
|sinx|dx=- sinxdx+
sinxdx+ sinxdx-
sinxdx-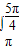 sinxdx
sinxdx
=cosx -cosx
-cosx  +cosx
+cosx  =1+2+(-
=1+2+(- +1)=4-
+1)=4-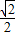 .
.
点评:本题主要考查了定积分在求面积中的应用,运用微积分基本定理计算定积分的关键是找到被积函数的原函数,属于基础题.
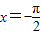 ,
, ,y=0所围成的平面图形的面积
,y=0所围成的平面图形的面积解答:解:s=
 |sinx|dx=-
|sinx|dx=- sinxdx+
sinxdx+ sinxdx-
sinxdx-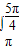 sinxdx
sinxdx=cosx
 -cosx
-cosx  +cosx
+cosx  =1+2+(-
=1+2+(- +1)=4-
+1)=4-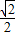 .
.点评:本题主要考查了定积分在求面积中的应用,运用微积分基本定理计算定积分的关键是找到被积函数的原函数,属于基础题.

练习册系列答案
相关题目
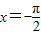 ,
,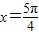 ,y=0所围成的平面图形的面积.
,y=0所围成的平面图形的面积.