题目内容
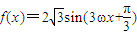 (ω>0)
(ω>0)(1)若f (x+θ)是周期为2π的偶函数,求ω及θ值.
(2)f (x)在(0,
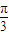 )上是增函数,求ω最大值.
)上是增函数,求ω最大值.
【答案】分析:(1)由f(x+θ)=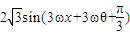 ,ω>0是周期为2π的偶函数,利用周期公式及诱导公式得2π=
,ω>0是周期为2π的偶函数,利用周期公式及诱导公式得2π=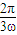 ,
,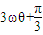 =
=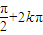 ,k∈Z,可解.
,k∈Z,可解.
(2)由正弦函数的单调性结合条件可列3ω×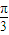 ≤
≤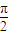 ,从而解得ω的取值范围,即可得ω的最大值.
,从而解得ω的取值范围,即可得ω的最大值.
解答:解:(1)因为f(x+θ)=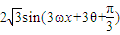 ,ω>0
,ω>0
又f(x+θ)是周期为2π的偶函数,
∴2π=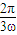 ,
,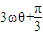 =
=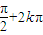 ,k∈Z
,k∈Z
故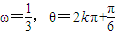 ,k∈Z
,k∈Z
(2)因为f(x)在(0,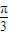 )上是增函数,
)上是增函数,
∴3ω×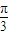 +
+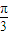 ≤
≤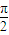 ∴ω≤
∴ω≤
故ω最大值为
点评:本题考查了y=Asin(ωx+φ)中参数的物理意义,及正弦函数的奇偶性与单调性,是个基础题.
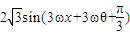 ,ω>0是周期为2π的偶函数,利用周期公式及诱导公式得2π=
,ω>0是周期为2π的偶函数,利用周期公式及诱导公式得2π=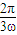 ,
,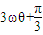 =
=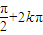 ,k∈Z,可解.
,k∈Z,可解.(2)由正弦函数的单调性结合条件可列3ω×
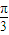 ≤
≤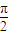 ,从而解得ω的取值范围,即可得ω的最大值.
,从而解得ω的取值范围,即可得ω的最大值.解答:解:(1)因为f(x+θ)=
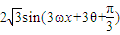 ,ω>0
,ω>0又f(x+θ)是周期为2π的偶函数,
∴2π=
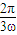 ,
,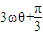 =
=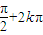 ,k∈Z
,k∈Z故
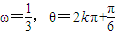 ,k∈Z
,k∈Z(2)因为f(x)在(0,
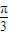 )上是增函数,
)上是增函数,∴3ω×
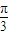 +
+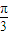 ≤
≤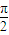 ∴ω≤
∴ω≤
故ω最大值为

点评:本题考查了y=Asin(ωx+φ)中参数的物理意义,及正弦函数的奇偶性与单调性,是个基础题.

练习册系列答案
相关题目