题目内容
已知
=cosα-sinα,则α取值范围是
| 1-2sinαcosα |
[2kπ-
,2kπ+
],k∈Z
| 3π |
| 4 |
| π |
| 4 |
[2kπ-
,2kπ+
],k∈Z
.| 3π |
| 4 |
| π |
| 4 |
分析:已知等式左边被开方数变形后,利用二次根式的化简公式化简,再利用绝对值的代数意义变形,根据正弦与余弦函数图象即可求出α的范围.
解答:解:∵
=
=|cosα-sinα|=cosα-sinα,
∴cosα>sinα,
则α的取值范围是[2kπ-
,2kπ+
],k∈Z.
故答案为:[2kπ-
,2kπ+
],k∈Z
| 1-2sinαcosα |
| (cosα-sinα)2 |
∴cosα>sinα,
则α的取值范围是[2kπ-
| 3π |
| 4 |
| π |
| 4 |
故答案为:[2kπ-
| 3π |
| 4 |
| π |
| 4 |
点评:此题考查了同角三角函数间的基本关系,以及三角函数的化简求值,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
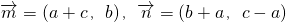 ,若
,若 ,求∠A.
,求∠A.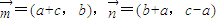 ,若
,若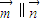 ,求∠A.
,求∠A.